
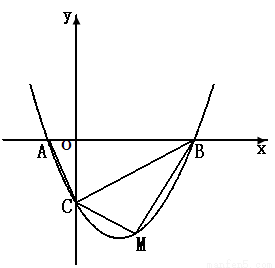
如图,二次函数 的图象与
的图象与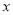 轴交于
轴交于 、
、 两点,与
两点,与 轴交于
轴交于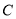 点,已知点
点,已知点 (-1,0),点C(0,-2).
(-1,0),点C(0,-2).
(1)求抛物线的函数解析式;
(2)试探究 的外接圆的圆心位置,并求出圆心坐标;
的外接圆的圆心位置,并求出圆心坐标;
(3)此抛物线上是否存在点P,使得以P、A、C、B为顶点的四边形为梯形.若存在,请写出所有符合条件的P点坐标;若不存在,请说明理由;
(4)若点 是线段
是线段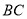 下方的抛物线上的一个动点,求
下方的抛物线上的一个动点,求 面积的最大值以及此时点
面积的最大值以及此时点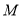 的坐标.
的坐标.
(1) 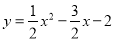 (2) 外接圆的圆心为AB的中点,且坐标为(
(2) 外接圆的圆心为AB的中点,且坐标为(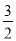 ,0).(3) P1(3,-2)、P2(5,3)、P3(-5,18) (4) 点M(2,﹣3),△MBC面积最大值是4.
,0).(3) P1(3,-2)、P2(5,3)、P3(-5,18) (4) 点M(2,﹣3),△MBC面积最大值是4.
【解析】
试题分析:(1)把点 (-1,0),点C(0,-2)代入解析式,即可求出a、c的值,从而二次函数的解析式可求;
(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
(3)根据梯形的定义即可求出点P的坐标;
(4)△MBC的面积可由S△MBC=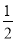 BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
(1)将A(-1,0)、点C(0,-2).代入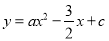
求得: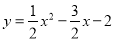
(2)∵A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,又:OC⊥AB,
∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
外接圆的圆心为AB的中点,且坐标为(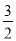 ,0).
,0).
(3)共三个P1(3,-2)、P2(5,3)、P3(-5,18)
(4)已求得:B(4,0)、C(0,-2),可得直线BC的解析式为:y=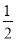 x-2;
x-2;
设直线l∥BC,则该直线的解析式可表示为:y=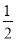 x+b,
x+b,
当直线l与抛物线只有一个交点时,可列方程:
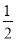 x+b=
x+b=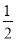 x2-
x2-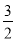 x-2,即:
x-2,即: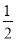 x2-2x-2-b=0,且△=0;
x2-2x-2-b=0,且△=0;
∴4-4×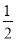 (-2-b)=0,即b=-4;
(-2-b)=0,即b=-4;
∴直线l:y=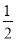 x-4.
x-4.
所以点M即直线l和抛物线的唯一交点,有:
 ,
,
解得: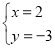
即 M(2,-3).
过M点作MN⊥x轴于N,
S△BMC=S梯形OCMN+S△MNB-S△OCB=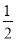 ×2×(2+3)+
×2×(2+3)+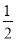 ×2×3-
×2×3-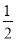 ×2×4=4.
×2×4=4.
∴点M(2,﹣3),△MBC面积最大值是4.
考点:二次函数综合题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源:2013-2014学年河北省保定市毕业生第一次模拟考试数学试卷(解析版) 题型:解答题
热气球的探测器显示,从热气球A看一栋高楼顶部B处的仰角为30º,看这栋高楼底部C处的俯角为60º,若热气球与高楼的水平距离为90 m,则这栋高楼有多高?(结果保留整数, ≈1.414,
≈1.414, ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期期中模拟考试数学试卷(解析版) 题型:选择题
如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E, .若
.若 ,
, ,则BD的长为( )
,则BD的长为( )

A、1 B、1.5 C、2 D、2.5
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:填空题
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程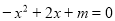 的解为 。
的解为 。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级下学期第一次段考数学试卷(解析版) 题型:选择题
小明随机地在对角线为6cm和8cm的菱形区域内投针,则针扎到其内切圆区域的概率是( )

A. B.
B. C.
C.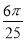 D.
D.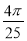
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:解答题
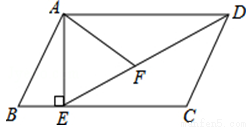
如图,在□ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4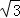 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:填空题
如图,M为双曲线 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴、x轴分别交于点A、B,则AD•BC的值为 ;
上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴、x轴分别交于点A、B,则AD•BC的值为 ;

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省苏州市高新区中考学二模数试卷(解析版) 题型:解答题
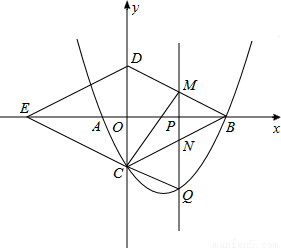
综合与探究:
如图,抛物线y= x2-
x2-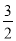 x-4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x-4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省盐城市亭湖区中考一模数学试卷(解析版) 题型:填空题
如图,边长为2正方形ABCD绕点A逆时针旋转45度后得到正方形 ,则在旋转过程中点D到D’的路径长是
,则在旋转过程中点D到D’的路径长是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com