
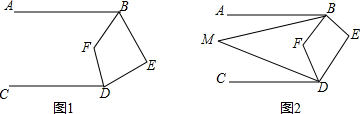
分析 (1)首先作EG∥AB,FH∥AB,利用平行线的性质可得∠ABE+∠CDE=280°,再利用角平分线的定义得到∠ABF+∠CDF=140°,从而得到∠BFD的度数;
(2)先由已知得到∠ABE=6∠ABM,∠CDE=6∠CDM,由(1)得∠ABE+∠CDE=360°-∠E,∠M=∠ABM+∠CDM,等量代换,即可.
解答  解:(1)如图1,作EG∥AB,FH∥AB,
解:(1)如图1,作EG∥AB,FH∥AB,
∵AB∥CD,
∴EG∥AB∥FH∥CD,
∴∠ABF=∠BFH,∠CDF=∠DFH,∠ABE+∠BEG=180°,∠GED+∠CDE=180°,
∴∠ABE+∠BEG+∠GED+∠CDE=360°
∵∠BED=∠BEG+∠DEG=80°,
∴∠ABE+∠CDE=280°,
∵∠ABF和∠CDF的角平分线相交于E,
∴∠ABF+∠CDF=140°,
∴∠BFD=∠BFH+∠DFH=140°;
(2)∵∠ABM=$\frac{1}{3}$∠ABF,∠CDM=$\frac{1}{3}$∠CDF,
∴∠ABF=3∠ABM,∠CDF=3∠CDM,
∵∠ABE与∠CDE两个角的角平分线相交于点F,
∴∠ABE=6∠ABM,∠CDE=6∠CDM,
∴6∠ABM+6∠CDM+∠E=360°,
∵∠M=∠ABM+∠CDM,
∴6∠M+∠E=360°.
点评 本题主要考查了平行线的性质和四边形的内角和,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
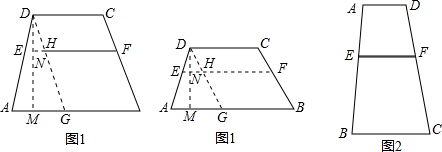 如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2.
如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
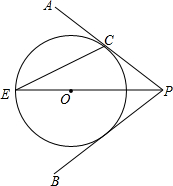 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
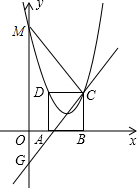 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2$\sqrt{3}$,直线y=$\sqrt{3}$x-2$\sqrt{3}$经过点C,交y轴于点G.
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2$\sqrt{3}$,直线y=$\sqrt{3}$x-2$\sqrt{3}$经过点C,交y轴于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
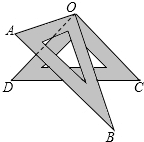 如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )
如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )| A. | ∠BOD | B. | ∠ABO | C. | ∠BOC | D. | ∠BAO |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
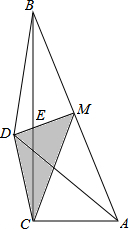 在△ABC中,AB=13,BC=12,CA=5,M是AB中点,点D与C在AB同侧,使DA=DB=7,则△CDM的面积为$\frac{357\sqrt{3}}{104}$.
在△ABC中,AB=13,BC=12,CA=5,M是AB中点,点D与C在AB同侧,使DA=DB=7,则△CDM的面积为$\frac{357\sqrt{3}}{104}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com