
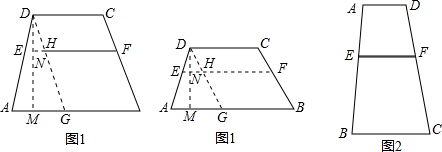
 如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2.
如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2.分析 作DG∥BC,交AB于G,交EF于点H,作DM⊥AB于点M,交EF于点N,则有HF=GB=CD=b,AG=AB-CD=a-b.易证,△DEH∽△DAG,可得$\frac{DN}{DM}$=$\frac{EH}{AG}$,即$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{EH}{a-b}$,然后根据$\frac{{d}_{1}}{{d}_{2}}$的值求出$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$的值,从而求出EH,进而可求出EF(即EH+HF)的值.由于在求EF的值时用到AD、BC、AE、BE(AB-AE),因而可提出“水渠EF的长为多少米?”这个问题.
解答 解:[类比发现]作DG∥BC,交AB于G,交EF于点H,作DM⊥AB于点M,交EF于点N.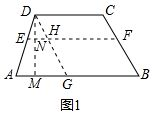
显然HF=GB=CD=b,AG=AB-CD=a-b.
易证,△DEH∽△DAG,可得$\frac{DN}{DM}$=$\frac{EH}{AG}$,
即$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{EH}{a-b}$,
而由$\frac{{d}_{1}}{{d}_{2}}$=$\frac{2}{1}$,得$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{2}{2+1}$=$\frac{2}{3}$,
代入$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{EH}{a-b}$,得$\frac{2}{3}$=$\frac{EH}{a-b}$.
解得:EH=$\frac{2}{3}$(a-b),
∴EF=EH+HF=$\frac{2}{3}$(a-b)+b=$\frac{2a+b}{3}$.
同理:当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{3}{1}$时,EF=$\frac{3a+b}{4}$;
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{n}$时,EF=$\frac{a+nb}{n+1}$;
当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{1}$时,EF=$\frac{ma+b}{m+1}$;
故答案分别为:$\frac{2a+b}{3}$、$\frac{3a+b}{4}$、$\frac{a+nb}{n+1}$、$\frac{ma+b}{m+1}$;
[推广证明]当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{n}$时,EF=$\frac{ma+nb}{m+n}$.
证明:作DG∥BC,交AB于G,交EF于点H,作DM⊥AB于点M,交EF于点N.
则有HF=GB=CD=b,AG=AB-CD=a-b.
易证,△DEH∽△DAG,可得$\frac{DN}{DM}$=$\frac{EH}{AG}$,
即$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{EH}{a-b}$,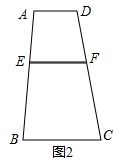
而由$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{n}$,得$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{m}{m+n}$,
代入$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{EH}{a-b}$,得$\frac{m}{m+n}$=$\frac{EH}{a-b}$.
解得:EH=$\frac{m}{m+n}$(a-b),
∴EF=EH+HF=$\frac{m}{m+n}$(a-b)+b=$\frac{ma+nb}{m+n}$.
故答案为:$\frac{ma+nb}{m+n}$;
[问题]水渠EF的长为多少米?
故答案为:水渠EF的长为多少米?.
点评 本题考查了相似三角形的判定和性质,平行线分线段成比例,突出了对提出问题的能力以及运用已有经验解决问题的能力的考查,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
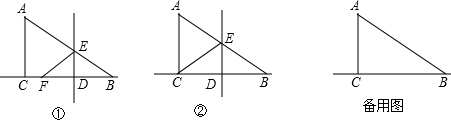
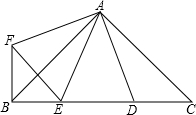 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )| A. | △AED≌△AEF | B. | △ABE∽△ACD | C. | BE+DC>DE | D. | BE2+DC2=DE2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
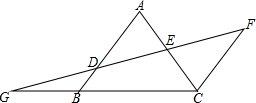 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com