练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知A=2x2-3x+1，B=3x2+2x-4，求3A-2B．

    分析 把A与B代入3A-2B中，去括号合并即可得到结果．

    解答 解：∵A=2x2-3x+1，B=3x2+2x-4，
    ∴3A-2B=3（2x2-3x+1）-2（3x2+2x-4）=6x2-9x+3-6x2-4x+8=-13x+11．

    点评 此题考查了整式的加减，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

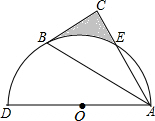    6．如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E．点B、E恰好是半圆弧的三等分点．若AD=4，则图中阴影部分的面积为$\frac{3\sqrt{3}}{2}$-$\frac{2π}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

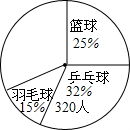    7．为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱，小李采用了抽样调查，在绘制扇形图时，由于时间仓促，还有足球、网球等信息还没有绘制完成，如图所示，根据图中的信息，这批被抽样调查的学生最喜欢足球的人数不可能是（　　）
    A．100人B．200人C．260人D．400人

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．化简：
    （1）3x2+[2x-（-5x2+4x）+2]-1．
    （2）y2+（x2+2xy-3y2）-（2x2-xy-2y2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：（-$\frac{1}{2}$）-2-16÷（-2）3+（$\sqrt{3}$-2）0-$\sqrt{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

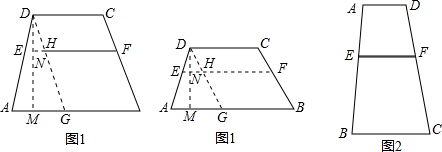    3．如图1，四边形ABCD中，AB∥CD，AB=a，CD=b（a≠b），点E、F分别是AD、BC上的点，且EF∥AB，设EF到CD、AB的距离分别为d1、d2．
    [初步尝试]
    小亮同学在对这一图形进行研究时，发现如下事实：
    （1）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{1}$时，有EF=$\frac{a+b}{2}$；
    （2）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{2}$时，有EF=$\frac{a+2b}{3}$．
    该同学思考研究（2）的过程如下：
    作DG∥BC，交AB于G，作DM⊥AB于点M，交EF于点N．
    显然HF=CD=b，AG=AB-CD=a-b．
    易证，△DEH∽△DAG，可得$\frac{DN}{DM}$=$\frac{EH}{AG}$，
    即，$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{EH}{a-b}$
    而由$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{2}$，得$\frac{{d}_{1}}{{d}_{1}{+d}_{2}}$=$\frac{1}{1+2}$=$\frac{1}{3}$，
    代入上式，则$\frac{1}{3}$=$\frac{EH}{a-b}$．
    解得EH=$\frac{1}{3}$（a-b）
    ∴EF=EH+HF=b+$\frac{1}{3}$（a-b）=$\frac{a+2b}{3}$
    [类比发现]
    沿用上述图形和已知条件，请自主完成进一步的研究发现：
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{2}{1}$时，EF=$\frac{2a+b}{3}$；
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{3}{1}$时，EF=$\frac{3a+b}{4}$；
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{n}$时，EF=$\frac{a+nb}{n+1}$；
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{1}$时，EF=$\frac{ma+b}{m+1}$．（其中m、n均为正整数，下同）
    [推广证明]
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{n}$时，EF=$\frac{ma+nb}{m+n}$；
    请证明你的结论．
    [实际应用]
    请结合所给情景，创设一个需要采用下面的全部信息求解的问题．
    [情景]
    如图2，有一块四边形耕地ABCD，AD∥BC，AD=100米，BC=300米，AB=500米，在AB上取点E，使AE=200米，以点E处为起点开挖平行于两底的水渠EF，与CD边相交于点F．
    [问题]
    水渠EF的长为多少米？（提问即可，不必求解）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

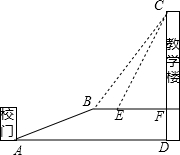    10．重庆是一座美丽的山坡，某中学依山而建，校门A处，有一斜坡AB，长度为13米，在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°，离B点4米远的E处有一花台，在E处仰望C的仰角∠CEF=63.4°，CF的延长线交校门处的水平面于D点，FD=5米．
    （1）求斜坡AB的坡度i．
    （2）求DC的长．
    （参考数据：tan53°≈$\frac{4}{3}$，tan63.4°≈2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

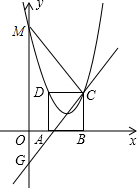    7．如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=2$\sqrt{3}$，直线y=$\sqrt{3}$x-2$\sqrt{3}$经过点C，交y轴于点G．
    （1）求C，D坐标；
    （2）已知抛物线顶点y=$\sqrt{3}$x-2$\sqrt{3}$上，且经过C，D，若抛物线与y交于点M连接MC，设点Q是线段下方此抛物线上一点，当点Q运动到什么位置时，△MCQ的面积最大？求出此时点Q的坐标和面积的最大值．
    （3）将（2）中抛物线沿直线y=$\sqrt{3}$x-2$\sqrt{3}$平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）．平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．把下列函数化成y=a（x-h）2+k的形式，并指出抛物线的开口方向，顶点坐标和对称轴，然后再用描点法画出函数图象．
    （1）y=2x2+8x+5；
    （2）y=-3x2+6x．

    查看答案和解析>>

    同步练习册答案