

���� ��1����A��-1��4������y=x2+bx���b���ٰ�B��a��0�����������ߵĽ���ʽ���ɽ�����⣮
��2����ͼ1�У���MG��y�ύAB��G����M��x��x2-3x������G��m��-m+3��������S��ABM=S��AMG+S��BMG�������κ��������ö��κ��������ʽ�����⣮
��3��������������ͼ2�У�����AE��ֻҪ֤���ı���APCE��ƽ���ı��Σ����ɽ�����⣮����ͼ3�У���PB=BCʱ������ͼ4�У���P��M�غ�ʱ����֤�ı���AEPC��ƽ���ı��Σ���EPC���APC�ص����ֵ�����ǡ�ABP�������$\frac{1}{4}$������ͼ4�У���P��M�غ�ʱ����֤�ı���AEPC��ƽ���ı��Σ���EPC���APC�ص����ֵ�����ǡ�ABP�������$\frac{1}{4}$���ֱ���⼴�ɣ�
��� �⣺��1����A��-1��4������y=x2+bx�õ�4=1-b��
��b=-3��
��y=x2-3x��
��B��a��0���ں���ͼ���ϣ�
��a2-3a=0��
��a=3��0����������
��a=3��
��2����ͼ1�У���MG��y�ύAB��G��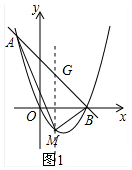
��ֱ��AB����ʽΪy=kx+b���ѣ�-1��4������3��0�������$\left\{\begin{array}{l}{-k+b=4}\\{3k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
��y=-x+3����M��x��x2-3x������G��m��-m+3����
��S��ABM=S��AMG+S��BMG=$\frac{1}{2}$��4��[��-x+3��-��x2-3x��=-2x2+4x+6=-2��x-1��2+8��
��-2��0��
�൱x=1ʱ����ABM�����������ֵΪ8��
��ʱM��1��-2����
��3������ͼ2�У�����AE��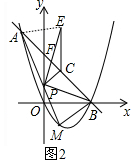
��CΪAB�е㣬��EPC���APC�ص����ֵ�����ǡ�ABP�������$\frac{1}{4}$��
��FΪAC��EP���е㣬����AE��
���ı���APCE��ƽ���ı��Σ�
��AP=EC=BC=$\frac{1}{2}$AB=2$\sqrt{2}$��
����ͼ3�У���PB=BCʱ��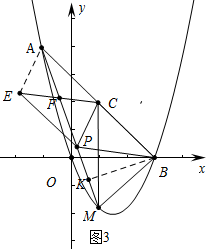
��PB=BC=EC=PE��
���ı���BCEP�����Σ�
��PE��BC����PE=AC��
���ı���AEPC��ƽ���ı��Σ���ʱ��EPC���APC�ص����ֵ�����ǡ�ABP�������$\frac{1}{4}$��
��BK��PM��K��
��AB=4$\sqrt{2}$��BM=2$\sqrt{2}$��AM=2$\sqrt{10}$��
��AM2=AB2+BM2��
���ABM=90�㣬
��$\frac{1}{2}$•BM•AB=$\frac{1}{2}$•AM•BK��
��BK=$\frac{BM•AB}{AM}$=$\frac{2\sqrt{2}•4\sqrt{2}}{2\sqrt{10}}$=$\frac{4}{5}$$\sqrt{10}$��
��PB=BM=2$\sqrt{2}$��
��PK=KM=$\sqrt{B{M}^{2}-B{K}^{2}}$=$\frac{2}{5}$$\sqrt{10}$��
��AK=$\sqrt{A{B}^{2}-B{K}^{2}}$=$\frac{8}{5}$$\sqrt{10}$��
��AP=AK=PK=$\frac{8}{5}$$\sqrt{10}$-$\frac{2}{5}$$\sqrt{10}$=$\frac{6}{5}$$\sqrt{10}$��
����ͼ4�У���P��M�غ�ʱ����֤�ı���AEPC��ƽ���ı��Σ���EPC���APC�ص����ֵ�����ǡ�ABP�������$\frac{1}{4}$����ʱAP=AM=2$\sqrt{10}$��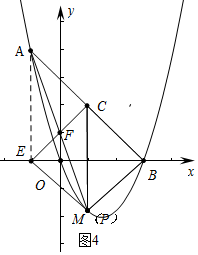
������������AP=2$\sqrt{2}$��$\frac{6}{5}$$\sqrt{10}$��2$\sqrt{10}$ʱ����EPC���APC�ص����ֵ�����ǡ�ABP�������$\frac{1}{4}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����ƽ���ı��ε��ж������ʵ�֪ʶ������Ĺؼ������������Щ֪ʶ������⣬ѧ�ṹ�����κ��������ֵ���⣬ע�ⲻ��©�⣬�����п�ѹ���⣮


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{{x}_{1}=-5}\\{{y}_{1}=2}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=-5}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{{x}_{1}=5}\\{{y}_{1}=2}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=5}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{{x}_{1}=5}\\{{y}_{1}=-2}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=5}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{{x}_{1}=-5}\\{{y}_{1}=-2}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-5}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}+1$ | B�� | $\sqrt{2}+1$ | C�� | $\sqrt{2}$ | D�� | $\sqrt{2}-1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����P������ABCD�Խ���AC�ϵ�һ�㣬����DP���ӳ�DP����AB�ڵ�E������BP���ӳ�����AD�ڵ�F����CD���ӳ����ڵ�G��
��ͼ����P������ABCD�Խ���AC�ϵ�һ�㣬����DP���ӳ�DP����AB�ڵ�E������BP���ӳ�����AD�ڵ�F����CD���ӳ����ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������a��b��Ӧ�ĵ��������ϵ�λ����ͼ��ʾ������|a-b|-2|a+1|-|b+1|��
��֪������a��b��Ӧ�ĵ��������ϵ�λ����ͼ��ʾ������|a-b|-2|a+1|-|b+1|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com