Question

15．如图，在矩形ABCD中，AD=2，CD=4，BN=2AM=2MN；点P为CD上的一动点（不与C、D重合），AP交DM于点E，PN交CM于点F，设DP=x．
（1）试用含x的式子表示：AE：AP的比值．
（2）请用含x的式子表示：△AME的面积．
（3）当DP为何值时，四边形PEMF的面积是矩形ABCD面积的$\frac{5}{32}$，并判断此时四边形DMNP的形状．

Answer 1

分析 （1）先求出AM=1，再根据△AEM∽△PED即可得出结论；
（2）先求出△AEM和△PED的对应边AM，PD上高的关系，利用它们的和2，得出AM边上的高，即可得出结论；
（3）同（2）得出S_△MFN=$\frac{1}{5-x}$，利用面积关系求出PD，分两种情况讨论计算即可得出结论．

解答 解：（1）在矩形ABCD中，AB=CD=4，BC=AB=2，AB∥DC
∵BN=2AM=2MN，
∴AM=$\frac{1}{4}$AB=1，
∵AB∥CD，
∴△AEM∽△PED，
∴$\frac{AE}{PE}=\frac{AM}{DP}$，
∵DP=x，
∴$\frac{AE}{PE}=\frac{1}{x}$，
∴$\frac{AE}{AP}=\frac{1}{x+1}$
（2）设△AEM的AM边山的高为h，△PED的PD边上的高为h'，
∴h+h'=AD=2
由（1）知，△AEM∽△PED，
∴$\frac{h}{h'}=\frac{AM}{DP}=\frac{1}{x}$，
∴h=$\frac{2}{x+1}$
∵S_△AEM=$\frac{1}{2}$AM×h=$\frac{1}{2}$×1×$\frac{2}{x+1}$=$\frac{1}{x+1}$，
（3）解：连接PM，设DP=x，则PC=4-x，
由（2）知，S_△AEM=$\frac{1}{x+1}$，
同（2）的方法得出S_△MFN=$\frac{1}{5-x}$
∵S_△APN=$\frac{1}{2}$AN×AD=2
∴S_{四边形PEMF的面积}=S_△APN-S_△AEM-S_△MFN=2-$\frac{1}{x+1}$-$\frac{1}{5-x}$
∵S_{四边形ABCD}=2×4=8，
而四边形PEMF的面积是矩形ABCD面积的$\frac{5}{32}$，
∴2-$\frac{1}{x+1}$-$\frac{1}{5-x}$=$\frac{5}{32}×8$=$\frac{5}{4}$，
∴x=1或x=3，
当x=1时，则有PD=MN，
∵PD∥MN，
∴四边形DMNP是平行四边形；
当x=3时，则PD=3，
∴PC=1，
如备用图，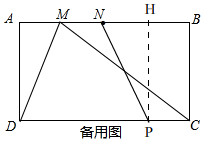

过点P作PH⊥AB，
∴NH=BH=1，
根据勾股定理得出PN=$\sqrt{5}$，
在Rt△ADM中，DM=$\sqrt{5}$，
∴DM=PN，
∵MN∥DP，MN≠DP，
∴四边形DMNP是等腰梯形．

点评 此题是四边形综合题，主要考查了矩形的性质，相似三角形的性质和判定，勾股定理，平行四边形的判定，等腰梯形的判定，求出S_△AEM=$\frac{1}{x+1}$是解本题的关键．