
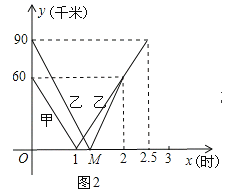
����Ŀ����ͼ,��һ����ֱ�ع�·����A,B,C����,,�������150km,�ס������������ֱ��B,C����ͬʱ����,�ع�·�����������,�ֱ�ʻ��C,B����.�ס���������A�صľ���y1��y2����ʻʱ��x(h)�ĺ���ͼ����ͼ2��ʾ.(��:����)
(1)����ͼ1�б��A�صĴ���λ��;
(2)ͼ2��,M���������_________,�õ��ʵ��������_________;
(3)��׳���A�صľ���![]() ����ʻʱ��
����ʻʱ��![]() �ĺ�����ϵʽ,ֱ��д���ҳ���A�صľ���y2����ʻʱ��
�ĺ�����ϵʽ,ֱ��д���ҳ���A�صľ���y2����ʻʱ��![]() �ĺ�����ϵʽ,����ͼ2�в�ȫ�׳��ĺ���ͼ��;
�ĺ�����ϵʽ,����ͼ2�в�ȫ�׳��ĺ���ͼ��;
(4)A������ָ������,ָ���������������жԽ���,�����Խ�����֮15km��(��15km)ʱ�ܹ�����ͨ��,ֱ��д����������ͬʱ��ָ�������öԽ���ͨ����ʱ��.


���𰸡���1�������������2����1.2��0������M��ʾ�ҳ�1.2Сʱ����A�أ���3���ף�0��x��1ʱ��y1=-60x+60��1��x��2.5ʱ��y1=60x-60���ң�0��x��1.2ʱ��y2=-75x+90��1.2��x��2ʱ��y2=75x-90��ͼ�����������4��![]() Сʱ.
Сʱ.
����������������� ��1������ͼ��ɵ�AB=60ǧ�ף�CA=90ǧ�ף�����AB��AC=2��3ȷ������A��λ�ü��ɣ���2��ֱ�Ӹ���������ʽ�����ҳ����ٶ�150��2=75ǧ��/ʱ��90��75=1.2�����Ե�M��ʾ�ҳ�1.2Сʱ����A�أ��ɴ˼�����⣻��3������ͼ���֪ͼ���ϵ�����꣬���������Ա���ȡֵ��Χ���������ϵʽ���ɣ���4�����ݡ������Խ�����15ǧ��֮�ڣ���15ǧ�ף�ʱ�ܹ�����ͨ������Ϊ���ȹ�ϵ�в���ʽ�飬��⼴�ɵõ�ͨ����ʱ�䷶Χ������������ͬʱ��ָ������ͨ����ʱ�䣮
���������
��1��A��λ����ͼ��ʾ��ʹ��A����AB��AC=2��3��
![]()
��2���ҳ����ٶ�150��2=75ǧ��/ʱ��
90��75=1.2��
��M��1.2��0����
���Ե�M��ʾ�ҳ�1.2Сʱ����A�أ�
��3���׳��ĺ���ͼ����ͼ��ʾ���׳����ٶ�60��1=60��ǧ��/ʱ����
�׳���B��C����ʱ��Ϊ��150��60=2.5��Сʱ����
����0��60������1��0��������y1=kx+b��
�ã� ![]() ��
��
��ã� ![]() ��
��
�ʵ�0��x��1ʱ��y1=-60x+60��
����2.5��90������1��0��������y1=ax+c��
![]() ��
��
��ã�
![]() .
.
�ʵ�1��x��2.5ʱ��y1=60x-60��
�ҳ���A�صľ���y2����ʻʱ��x��h���ĺ�����ϵʽΪ��
����0��90������1.2��0��������y2=dx+e��
![]() ��
��
��ã� ![]() ��
��
�ʵ�0��x��1.2ʱ��y2=-75x+90��
����2��60������1.2��0��������y2=fx+r��
![]() ��
��
��ã� ![]() ��
��
�ʵ�1.2��x��2ʱ��y2=75x-90��
��ͼ��ʾ��
 ��
��
��4��������ü׳���ָ�����ĵ�ͨ��ʱ��Ϊ�� ![]() ��
��
��![]() ��x��
��x��![]() ��
��
�ҳ���ָ�����ĵ�ͨ��ʱ�䣺
![]() ��
��
��1��x��![]() ��
��
��1��x��![]() ��
��
������ͬʱ��ָ������ͨ����ʱ��Ϊ: ![]() -1=
-1=![]() Сʱ��
Сʱ��


 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�鳤����ľ��ĸ��ⳤ��ͼ��ʾ��һֻ֩����ľ���һ������A����һֻ��Ӭ������������Ϻ�֩����ԵĶ���B����֩�뼱��ס��Ӭ�����ų�����ı�����������
(1)���D������е㣬֩������AD��DB��·�����У�����A������B�����ߵ�·��Ϊ���٣�
(2)����Ϊ��AD��DB�������·�����������Ϊ���ǣ���������̵�·�̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���kx2����3k��1��x+2��k��1��=0
��1����֤������kΪ�κ�ʵ������������ʵ������
��2�����˷���������ʵ����x1 �� x2 �� ��|x1��x2|=2����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����F�ڱ�AC�ϣ�����CF=2����EΪ��BC�ϵĶ��㣬����CEF��ֱ��EF���ۣ���C���ڵ�P�������P����AB�������Сֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�ĶԽ��߽��ڵ�E����AE=EC��BE=ED����ABΪֱ���İ�Բ����E��Բ��ΪO��
��1������ͼ1����֤���ı���ABCD�����Σ� 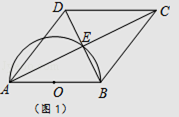
��2����ͼ2����CD���ӳ������Բ�����ڵ�F����ֱ֪��AB=8�� ������OE�����OBE�������
��������AOE�������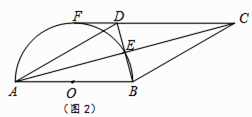
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������:
(1) (��4x2y)��(��x2y2)��(![]() y)3�� (2) (��3ab)(2a2b��ab��1) ��
y)3�� (2) (��3ab)(2a2b��ab��1) ��
(3) (m��![]() )(m��
)(m��![]() )�� ��4�� ��-x-1��(-x+1) �� (5) ( - x - 5)2 �� ��6��
)�� ��4�� ��-x-1��(-x+1) �� (5) ( - x - 5)2 �� ��6��![]() ��
��
��7���Ȼ���������ֵ����x+1��2����x+2����x��2��������![]() ��
��
(8)�ⷽ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֵ��֤��
��![]() ��0��1��2��5����ʱ���������ʽ
��0��1��2��5����ʱ���������ʽ![]() ��ֵ���ֱ�õ�5��2��1��2��17��������x��ȡֵ�����仯ʱ������ʽ
��ֵ���ֱ�õ�5��2��1��2��17��������x��ȡֵ�����仯ʱ������ʽ![]() ��ֵȴ��һ��ȷ���ķ�Χ��ͨ�������֤���Է�������ֵ�ܴ��ڻ����1������1����������Сֵ��
��ֵȴ��һ��ȷ���ķ�Χ��ͨ�������֤���Է�������ֵ�ܴ��ڻ����1������1����������Сֵ��
��ʽ��֤��
���ǿ�����ѧ����֪ʶ����![]() ���к�ȱ��Σ�
���к�ȱ��Σ�![]() ����ע�����ֱ��η����ɳ�Ϊ���䷽����
����ע�����ֱ��η����ɳ�Ϊ���䷽���� ![]() ��
��![]() ����������xȡ��ֵ������ʽ
����������xȡ��ֵ������ʽ![]() ��ֵ��С��1������СֵΪ1��
��ֵ��С��1������СֵΪ1��
Ǩ��ʵ֤��
��1�����������䷽���ķ�����ȷ��![]() ����СֵΪ3��
����СֵΪ3��
��2����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��![]() ���ֿ�ֱ��л���16̨��12̨����Ҫ�����ס������أ����м���Ҫ15̨���ҵ���Ҫ13̨����֪
���ֿ�ֱ��л���16̨��12̨����Ҫ�����ס������أ����м���Ҫ15̨���ҵ���Ҫ13̨����֪![]() ���زֿ������ף������ػ����ķ���������������ʾ��
���زֿ������ף������ػ����ķ���������������ʾ��
![]() ���A�ֿ��x̨����ȥ�أ����ú�x�Ĵ���ʽ��ȫ������ұ���
���A�ֿ��x̨����ȥ�أ����ú�x�Ĵ���ʽ��ȫ������ұ���
�������˷��ñ��������˷�����
������ Ŀ�ĵ��˷� | A | B | ������ Ŀ�ĵ����� | A | B | �ϼ� | |
�� | 500 | 300 | �� | x | 15 | ||
�� | 400 | 600 | �ҵ� | 13 | |||
�ϼ� | 16 | 12 | 28 |
![]() �����˷�ΪyԪ����y��x֮��ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
�����˷�ΪyԪ����y��x֮��ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
![]() �ɻ������˷�������֪����n�ֵ��˷�������n��ֵ��
�ɻ������˷�������֪����n�ֵ��˷�������n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ݲ����ڼ䣬���껪���ֳ�Ͷ��150��Ԫ����һ�����������ʩ��������ά�ޱ������ã�Ԥ�ƿ��ź�ÿ�¿ɴ���33��Ԫ������������ʩ���źӵ�1���µ���x���µ�ά�ޱ��������ۼ�Ϊy����Ԫ������y=ax2+bx���������տ۳�Ͷ�ʺ�ά�ޱ������ó�Ϊ���ֳ��Ĵ�����g����Ԫ����gҲ�ǹ���x�Ķ��κ�����
��1����ά�ޱ������õ�1����Ϊ2��Ԫ����2����Ϊ4��Ԫ����y����x�Ľ���ʽ��
��2��������g����x�Ľ���ʽ��
��3������ʩ���ż����º����ֳ��Ĵ�����ﵽ������º����ջ�Ͷ�ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com