
【题目】把长方形OABC放在如图所示的平面直角坐标系中,点F、E分别在边OA和AB上,若点F (0,3),点C (9,0),且∠FEC=90°,EF=EC,则点E的坐标为_____.

【答案】(6,6)
【解析】
根据矩形的性质得到AB=OC=9,∠FAE=∠B=90°,根据余角的性质得到∠AFE=∠CEB,根据全等三角形的性质得到AF=BE,AE=BC,设AF=BE=x,列方程即可得到结论.
解:∵点F (0,3),点C (9,0),
∴OF=3,OC=9,
∵四边形ABCO是矩形,
∴AB=OC=9,∠FAE=∠B=90°,
∵∠FEC=90°,
∴∠AEF+∠AFE=∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∵EF=EC,
∴△AEF≌△BCE(AAS),
∴AF=BE,AE=BC,
设AF=BE=x,
∴AO=BC=AE=x+3,
∴x+3+x=9,
∴x=3,
∴AE=BC=6,
∴点E的坐标为(6,6),
故答案为:(6,6).


科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
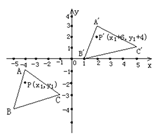
【题目】如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标。
(3)求△A′B′C′的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,CD=CB,点E为BD的中点,且EA=EC,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=![]() AC;
AC;
(2)求线段AM、DM、BC之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE∶CE=3∶2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.
(1)线段AE=______;
(2)设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;
(3)当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有边长为1,a(a>1)的一张矩形纸片ABCD,把这个矩形按要求分割,画出分割线,并在相应的位置上写出a的值.
(1)把这个矩形分成两个全等的小矩形,且分成的两个矩形与原矩形相似.
(2)把这个和矩形分成三个矩形,且每一个矩形都与原矩形相似,给出两种不同的分割.

查看答案和解析>>
科目:初中数学 来源: 题型:
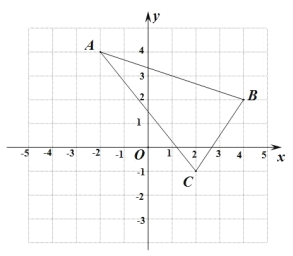
【题目】如图,△ABC 在平面直角坐标系中,点 A,B,C 的坐标分别为 A(-2,4),B(4,2),C(2,-1).
(Ⅰ)请在平面直角坐标系内,画出△ABC 关于 x 轴的对称图形△A1B1C1,其中,点 A,B,C 的对应点分别为A1,B1,C1;
(Ⅱ)请写出点C(2,-1)关于直线m(直线m上格点的横坐标都为-1)对称的点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
现有甲、乙两种机器加工零件,甲种机器比乙种机器每小时多加工30个,甲种机器加工900个零件所用时间与乙种机器加工600个零件所用时间相等,求两种机器每小时各加工多少个零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com