
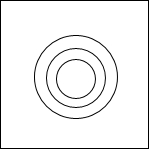
 某健身俱乐部设置了如图所示的一个投镖靶,该靶是边长为18cm的正方形木板,镖靶从中心往外依次画有半径分别为1cm、2cm和3cm的同心圆,当投镖者投中最里层最小的圆时,获得一等奖;当投中小圆与中间圆围成的圆环时,可获得二等奖;当投中中圆与最大的圆围成的圆环时,可获得三等奖.若每人只投一镖,请你分别求出获得第一名和第三名的概率.(结果精确到0.01)
某健身俱乐部设置了如图所示的一个投镖靶,该靶是边长为18cm的正方形木板,镖靶从中心往外依次画有半径分别为1cm、2cm和3cm的同心圆,当投镖者投中最里层最小的圆时,获得一等奖;当投中小圆与中间圆围成的圆环时,可获得二等奖;当投中中圆与最大的圆围成的圆环时,可获得三等奖.若每人只投一镖,请你分别求出获得第一名和第三名的概率.(结果精确到0.01)科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、(
| ||||
B、(-1,
| ||||
C、(
| ||||
D、(-
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com