
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
【答案】(1)16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;(2)![]()
【解析】(1)画树状图:

共有16种等可能的结果数,它们是:11,41,71,81,14,44,74,84,17,47,77,87,18,48,78,88;
(2)算术平方根大于4且小于7的结果数为6,
所以算术平方根大于4且小于7的概率=![]() =3/8.
=3/8.
【题型】解答题
【结束】
23
【题目】某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为____,图①中m的值是____;
(2)求本次你调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
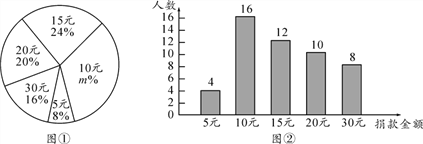
【答案】(1)50,32;(2)平均数是16,众数是10元,中位数是15元; (3) 928人.
【解析】分析:(1)由捐5元的4人占调查人数的8%求调查的总人数;捐10元的人数除以调查的总人数可求m;(2)根据平均数,众数,中位数的定义求解;(3)用调查人数中捐10元的百分比乘以本校人数.
详解:(1)本次接受随机抽样调查的学生人数为4÷8%=50(人);
因为![]() ×100%=32%,所以m=32.
×100%=32%,所以m=32.
故答案为50,32;
(2)平均数是![]() (4×5+16×10+12×15+10×20+8×30)=16(元),
(4×5+16×10+12×15+10×20+8×30)=16(元),
众数是10元,中位数是15元.
(3)该校本次活动捐款金额为10元的学生人数是2900×32%=928(人)


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】(11分)如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
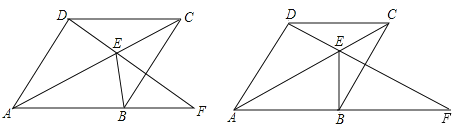
(1)如图①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学为了解自己居住的小区家庭生活用水情况,从中随机调查了其中![]() 的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.
的家庭一年的月平均用水量(单位:顿).并将调查结果制成了如图所示的条形和扇形统计图.
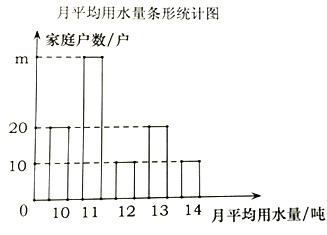
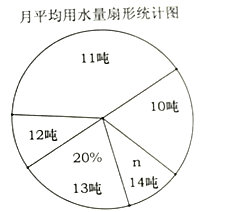
![]() 小明随机调查了 户家庭,该小区共有 户家庭;
小明随机调查了 户家庭,该小区共有 户家庭;
![]()
![]() ,
,![]() ;
;
![]() 这个样本数据的众数是 ,中位数是 ;
这个样本数据的众数是 ,中位数是 ;
![]() 根据样本数据,请估计该小区家庭月平均用水量不超过
根据样本数据,请估计该小区家庭月平均用水量不超过![]() 吨的有多少户?
吨的有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
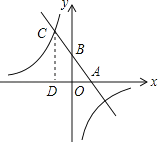
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
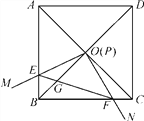
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:(1)EF=![]() OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OG·BD=AE2+CF2,其中正确的是__.
;(5)OG·BD=AE2+CF2,其中正确的是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com