
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.


(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3![]() .
.
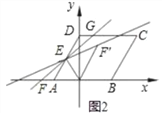
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
【答案】(Ⅰ)∠DAO=60°,DE=2; (Ⅱ)①GH=6,DG=﹣3+![]() ;②F(﹣5﹣
;②F(﹣5﹣![]() ,0).
,0).
【解析】解:(Ⅰ)∵A(﹣2,0),D(0,2![]() )∴AO=2,DO=2
)∴AO=2,DO=2![]() ,∴tan∠DAO=
,∴tan∠DAO=![]() =
=![]() ,
,
∴∠DAO=60°,∴∠ADO=30°,∴AD=2AO=4,∵点E为线段AD中点,∴DE=2;
(Ⅱ)①如图2,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DGE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,
∴∠EOF′=∠AEO,∴AD∥OF′,∴∠OF′E=∠DEH,∴∠DEH=∠DGE,
∵∠DEH=∠EDG,∴△DHE∽△DEG,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DG=x,则DH=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,∴DG=﹣3+
,∴DG=﹣3+![]() .
.
②如图3,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DHE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,∴∠EOF′=∠AEO,∴AD∥OF′,
∴∠OF′E=∠DEH,∴∠DEG=∠DHE,
∵∠DEG=∠EDH,∴△DGE∽△DEH,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DH=x,则DG=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,
,
∴DH=﹣3+![]() .∴DG=3+
.∴DG=3+![]() ∴DG=AF=3+
∴DG=AF=3+![]() ,∴OF=5+
,∴OF=5+![]() ,∴F(﹣5﹣
,∴F(﹣5﹣![]() ,0).
,0).


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC. 
(1)求证:AD=AE;
(2)若AD=8,DC=4,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强用8块棱长为3 cm的小正方体,搭建了一个如图所示的积木,下列说法中不正确的是( )

A. 从左面看这个积木时,看到的图形面积是27cm2
B. 从正面看这个积木时,看到的图形面积是54cm2
C. 从上面看这个积木时,看到的图形面积是45cm2
D. 分别从正面、左面、上面看这个积木时,看到的图形面积都是72cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代数学著作《九章数学》的“方程”一章,在世界数学史上首次正式引入负数,如果收入100元记作+100元,那么-80元表示( )
A.支出-80元B.收入80元C.支出80元D.收入20元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.

(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一中学组织七年级部分学生和老师到苏州乐园开展社会实践活动,租用的客车有50座和30座两种可供选择.学校根据参加活动的师生人数计算可知:若只租用30座客车x辆,还差5人才能坐满;
(1)则该校参加此次活动的师生人数为 (用含x的代数式表示);
(2)若只租用50座客车,比只租用30座客车少用2辆,求参加此次活动的师生至少有多少人?
(3)已知租用一辆30座客车往返费用为400元,租用一辆50座客车往返费用为600元,学校根据师生人数选择了费用最低的租车方案,总费用为2200元,试求参加此次活动的师生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC
证明:∵EF⊥AB CD⊥AB
∴∠EFA=∠CDA=90°(垂直定义)
∴EF∥CD
∴∠1=∠
∵∠1=∠2(已知)
∴∠2=∠ACD(等量代换)
∴DG∥AC
∴∠DGB=∠ACB
∵AC⊥BC(已知)
∴∠ACB=90°(垂直定义)
∴∠DGB=90°即DG⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在相同的条件下各射靶10次,每次命中的环数如下: 甲:9,7,8,9,7,6,10,10,6,8;
乙:7,8,8,9,7,8,9,8,10,6
(1)分别计算甲、乙两组数据的方差;
(2)根据计算结果比较两人的射击水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至2016年底,国家开发银行对“一代一路”沿线国家累计贷款超过1600亿美元,其中1600亿用科学记数法表示为( )
A.16×1010
B.1.6×1010
C.1.6×1011
D.0.16×1012
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com