
【题目】已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC
证明:∵EF⊥AB CD⊥AB
∴∠EFA=∠CDA=90°(垂直定义)
∴EF∥CD
∴∠1=∠
∵∠1=∠2(已知)
∴∠2=∠ACD(等量代换)
∴DG∥AC
∴∠DGB=∠ACB
∵AC⊥BC(已知)
∴∠ACB=90°(垂直定义)
∴∠DGB=90°即DG⊥BC.
【答案】见解析.
【解析】试题分析:已知EF⊥AB ,CD⊥AB,由垂直定义可得∠EFA=∠CDA=90°,由同位角相等,两直线平行可得EF∥CD,由两直线平行,同位角相等可得∠1=∠ACD,又因为已知∠1=∠2,等量代换得∠2=∠ACD,由内错角相等,两直线平行可得DG∥AC,由两直线平行,同位角相等可得∠DGB=∠ACB,已知AC⊥BC,由垂直定义可得∠ACB=90°,所以∠DGB=90°即DG⊥BC.
试题解析:
证明:∵EF⊥AB ,CD⊥AB(已知),
∴∠EFA=∠CDA=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠1=∠ACD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠2=∠ACD(等量代换)
∴DG∥AC(内错角相等,两直线平行),
∴∠DGB=∠ACB(两直线平行,同位角相等),
∵AC⊥BC(已知),
∴∠ACB=90°(垂直定义),
∴∠DGB=90°即DG⊥BC.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:如果ab=N(a>0,且a≠1),那么数b叫做以a为底N的对数,记作b=logaN.例如23=8,则log28=3.根据材料填空:log39=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.

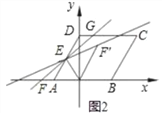

(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3![]() .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛运动员的成绩(单位:m),绘制出如下所示的条形统计图和扇形统计图,请根据统计图相关信息,解答下列问题: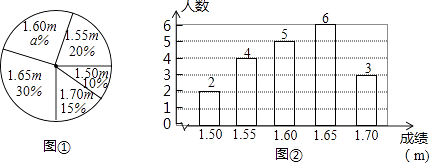
(1)求扇形统计图中a值;
(2)求男子跳高初赛成绩的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在比例尺为1:5000的地图上,量得甲、乙两地的距离是7厘米,则两地间的实际距离为( )
A.35米B.350米C.3500米D.35000米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
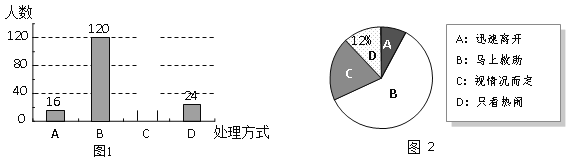
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
证明:∵∠1=∠2(_________),∠1=∠3 ,∠2=∠4(_____________),
∴∠3=∠4(_________).
∴____________∥____________(_______________).
∴∠C=∠ABD(_____________).
∵∠C=∠D(__________),
∴∠D=________(____________).
∴AC∥DF(_____________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售量可增加 20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢利市场,该店应按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com