
【题目】在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率为 ;
(2)从中先任取一球(不放回),将球上的数字记为a,再从中任取一球,将球上的数字记为b,求![]() 的概率(用列表或树状图说明理由).
的概率(用列表或树状图说明理由).
【答案】(1)![]() ;(2)列表见解析;
;(2)列表见解析; ![]()
【解析】试题分析:(1)直接根据概率公式求解即可;
(2)先利用树状图展示12种等可能的结果数,再得到ab>0的所有可能的数目,即可求出其概率.
试题解析:
(1)∵从数字-3、-1、0、2的四个小球中任意抽取一个数,共有4种可能,但其中为正数的2,
∴抽取的数字为正数的概率=![]() .
.
(2)画树状图得:
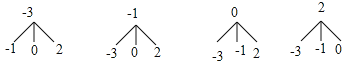
共有12种等可能的结果数,它们是:(-3,-1),(-3,0),(-3,2),(-1,-3),(-1,0),(-1,2),(0,-3),(0,-1),(0,2),(2,-3),(2,-1),(2,0),
其中ab>0的所有可能的结果有2种,所以ab>0的概率![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,三角形ABC内任意一点P(x0,y0),将三角形ABC平移后,点P的对应点为P1(x0+5,y0-3).
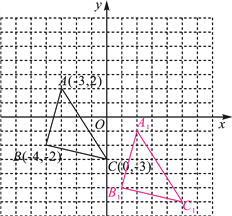
(1)写出将三角形ABC平移后,三角形ABC中A,B,C分别对应的点A1,B1,C1的坐标,并画出三角形A1B1C1;
(2)若三角形ABC外有一点M经过同样的平移后得到点M1(5,3),写出M点的坐标_______,若连接线段MM1,PP1,则这两条线段之间的关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是全国最大的瓷碗造型建筑坐落于江西景德镇,整体造型概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为了计算该建筑物的横断面(瓷碗横断面ABCD为等腰梯形)的高度如图2,她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°,而后沿着一段坡度为0.44的小坡PQ步行到点Q(此过程中AD、AP、PQ始终处于同一平面)后测得点D的仰角减少了5°.
已知坡PQ的水平距离为20米,小敏身高忽略不计.
(1)试计算该瓷碗建筑物的高度?
(2)小敏测得AD与水平面夹角约为58°,底座直径AB约为20米,试计算碗口CD的直径为多少米?
坡度:坡与水平线夹角的正切值.
参考数据:sin40°≈0.64,tan40°≈0.84,sin58°≈0.85,tan58°≈1.60.


![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有35名同学参加眉山市的三苏文化知识竞赛,预赛分数各不相同,取前18名同学参加决赛. 其中一名同学知道自己的分数后,要判断自己能否进入决赛,只需要知道这35名同学分数的( ).
A. 众数 B. 中位数 C. 平均数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市120000名初中学生的视力情况,某校数学兴趣小组,并进行整理分析.
(1)小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.
(2)该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
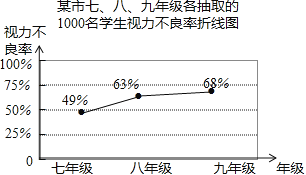
请你根据抽样调查的结果,估计该市120000名初中学生视力不良的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王班的同学去年6﹣12月区孔子学堂听中国传统文化讲座的人数如下表:
月份 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
人数 | 46 | 32 | 42 | 32 | 27 | 32 | 42 |
则该班去年6﹣12月去孔子学堂听中国传统文化讲座的人数的众数是( )
A.46
B.42
C.32
D.27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD各顶点的坐标分别为A(0,1),B(5,1),C(7,3),D(2,5).
(1)在平面直角坐标系中画出该四边形;
(2)四边形ABCD内(边界点除外)一共有________个整点(即横坐标和纵坐标都是整数的点);
(3)求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com