


科目:初中数学 来源: 题型:
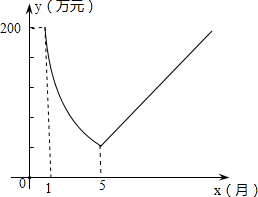 保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2014年1月的利润为200万元.设2014年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2014年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2014年1月的利润为200万元.设2014年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2014年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).查看答案和解析>>
科目:初中数学 来源: 题型:
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车装载量(吨) | 6 | 5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
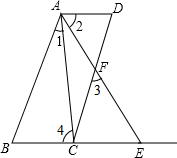 如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.
如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.查看答案和解析>>
科目:初中数学 来源: 题型:
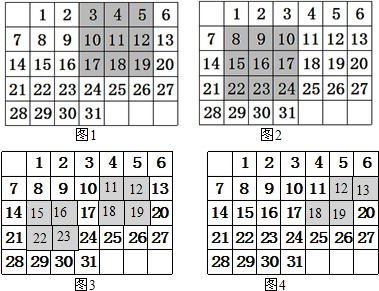
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com