
【题目】甲乙两地相距160千米,一辆汽车和一辆拖拉机同时由甲、乙两地相向而行,1小时20分相遇.相遇后,拖拉机继续前进,汽车在相遇处停留1个小时后调头按原速返回,汽车在返回后半个小时追上了拖拉机.
(1)在这个问题中,1小时20分= 小时;
(2)相向而行时,汽车行驶 小时的路程+拖拉机行驶 小时的路程=160千米;同向而行时,汽车行驶 小时的路程=拖拉机行驶 小时的路程;
(3)全程汽车、拖拉机各自行驶了多少千米?
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ,
,![]() ;(3)汽车行驶的路程为165千米,拖拉机行驶的路程为85千米.
;(3)汽车行驶的路程为165千米,拖拉机行驶的路程为85千米.
【解析】
(1)根据1小时=60分进行单位换算即可;
(2)相向而行,相遇时两者行驶时间相同,行驶距离之和为160千米,同向而行,汽车追上拖拉机时,汽车行驶时间为![]() 小时,拖拉机行驶
小时,拖拉机行驶![]() 小时,据此填写即可;
小时,据此填写即可;
(3)设汽车、拖拉机的速度分别是![]() 千米/小时,根据(2)中的等量关系建立方程求出汽车和拖拉机的速度,再用速度乘以行驶的总时间求出行驶路程.
千米/小时,根据(2)中的等量关系建立方程求出汽车和拖拉机的速度,再用速度乘以行驶的总时间求出行驶路程.
(1)20分=![]() 小时,
小时,
∴1小时20分=![]() 小时
小时
故答案为:![]() .
.
(2)相向而行,相遇时,两者行驶时间均为![]() 小时,同向而行,汽车追上拖拉机时,汽车行驶时间为
小时,同向而行,汽车追上拖拉机时,汽车行驶时间为![]() 小时,拖拉机行驶
小时,拖拉机行驶![]() 小时
小时
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(3) 解:设汽车、拖拉机的速度分别是![]() 千米/小时,依题意有:
千米/小时,依题意有:
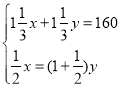 ,解之得:
,解之得:![]()
全程汽车行驶的路程为![]() (千米)
(千米)
全程拖拉机行驶的路程为![]() (千米)
(千米)
答:全程汽车行驶的路程为165千米,拖拉机行驶的路程为85千米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
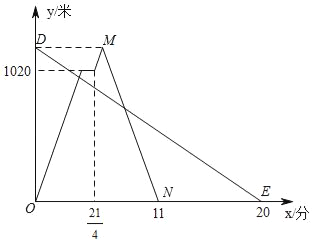
(1)请写出甲的骑行速度为 米/分,点M的坐标为 ;
(2)求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑电动车从甲地去乙地,而小刚骑自行车从乙地去甲地,两人同时出发走相同的路线;设小刚行驶的时间为x(h),两人之间的距离为y(km),图中的折线表示y与x之间的函数关系,点B的坐标为(![]() ,0). 根据图象进行探究:
,0). 根据图象进行探究:

(1)两地之间的距离为 km;
(2)请解释图中点B的实际意义;
(3)求两人的速度分别是每分钟多少km?
(4)求线段BC所表示的y与x之间的函数关系式;并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个周末,小丽从家去园博园参观,同时妈妈参观结束从园博园回家,小丽刚到园博园就发现要下雨,于是立即按原路返回,追上妈妈后,两人一同回家(小丽和妈妈始终在同一条笔直的公路上行走)如图是两人离家的距离y(米)与小丽出发的时间x(分)之间的函数图象,请根据图象信息回答下列问题:
(1)求线段BC的解析式;
(2)求点F的坐标,并说明其实际意义;
(3)与按原速度回家相比,妈妈提前了几分钟到家?并直接写出小丽与妈妈何时相距800米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=![]() .
.
(1)若反比例函数y=![]() (x>0)的图象经过AO的中点C,求k的值;
(x>0)的图象经过AO的中点C,求k的值;
(2)在(1)的条件下,若反比例函数y=![]() (x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(3)若点D关于y轴的对称点为E,当反比例函数y=![]() 的图象和线段AE有公共点时,直接写出k的取值范围.
的图象和线段AE有公共点时,直接写出k的取值范围.
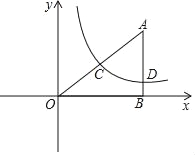
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
(1)线段AE=____________;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α=___________°时,DM与⊙O相切。
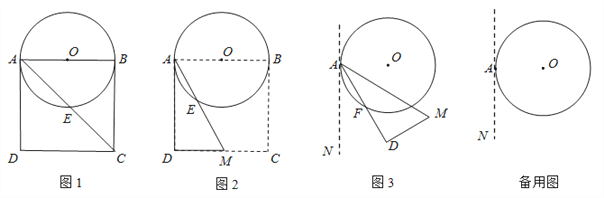
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
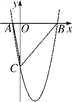
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx-5与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C,连接AC,BC.
(1)求抛物线的函数表达式;
(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com