
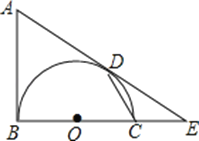
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;
(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论;
(3)根据已知条件得到∠DOC=2∠CDE=54°,根据平角的定义得到∠BOD=180°-54°=126°,然后由弧长的公式即可计算出结果.
试题解析:(1)连接OD,BD,
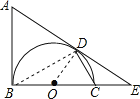
∵AB是⊙O的切线,∴AB⊥BC,即∠ABO=90°,
∵AB=AD,∴∠ABD=∠ADB,
∵OB=OD,∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,∴∠ADO=∠ABO=90°;
又∵OD是圆O的半径,∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD=∠COD
∵AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,∴∠DOC=2∠BDO=2∠CDE,
∴∠A=2∠CDE;
(3)解:∵∠CDE=27°,∴∠DOC=2∠CDE=54°,∴∠BOD=180°-54°=126°,
∵OB=2,∴![]()


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC, 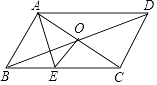
(1)若△ABE的周长为10cm,求平行四边形ABCD的周长,
(2)若∠DAB=108°,AE平分∠BAC,试求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.0000077米,将0.0000077用科学记数法表示为( )
A.7.7×10﹣6B.7.7×10﹣5C.0.77×10﹣6D.0.77×10﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
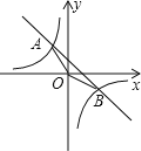
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M(2)=(-2)×(-2),
M(3)=(-2)×(-2)×(-2),
…,
M(n)= ![]() .
.
(1)计算:M(5)+M(6);
(2)求2M(2 016)+M(2 017)的值;
(3)说明2M(n)与M(n+1)互为相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22 015+22 016的值.
解:设S=1+2+22+23+24+…+22 015+22 016, ①
将等式两边同时乘2,得2S=2+22+23+24+25+…+22 016+22 017, ②
②-①,得2S-S=22 017-1,即S=22 017-1,
所以1+2+22+23+24+…+22 015+22 016=22 017-1.
请你仿照此法计算:
(1)1+2+22+23+24+…+29+210;
(2)1+3+32+33+34+…+3n-1+3n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.

解:∠B+∠E=∠BCE
过点C作CF∥AB,
则![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com