
【题目】如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC, 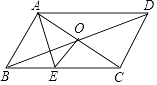
(1)若△ABE的周长为10cm,求平行四边形ABCD的周长,
(2)若∠DAB=108°,AE平分∠BAC,试求∠ACB的度数.
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴OA=OC.
∵OE⊥AC,
∴AE=CE.
∴△ABE的周长为AB+AC=10,
根据平行四边形的对边相等得,
平行四边形ABCD的周长为2×10=20cm.
(2)解:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵△ACE是等腰三角形,
∴∠CAE=∠ACB
∵四边形ABCD是平行四边形,
∴∠ACB=∠CAD,
∴∠DAB=∠BAE+∠CAE+∠CAD=3∠CAD=108°,
∴∠ACB=∠CAD=36°.
【解析】(1)根据平行四边形的对角线互相平分得:OA=OC.又OE⊥AC,根据线段垂直平分线上的点到线段两个端点的距离相等得:AE=CE.故△ABE的周长为AB+BC的长.最后根据平行四边形的对边相等得:ABCD的周长为2×10=20cm.(2)由已知条件和平行四边形的性质易求∠DAB=∠BAE+∠CAE+∠CAD=3∠CAD=108°,进而可求出∠ACB的度数.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
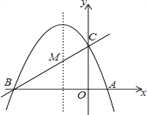
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的周长为1,连接△ABC的三边中点构成第二个三角形,再连接第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,求y与x之间的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0)。未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元。通过市场调研发现,该时装单价每降1元,每天销量增加4件。在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
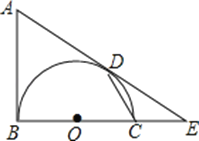
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com