
分析 (1)根据a=csinA、b=ccosA计算可得;
(2)根据sinA=$\frac{a}{c}$=$\frac{\sqrt{4}}{\sqrt{6}}$=$\frac{\sqrt{6}}{3}$、b=$\sqrt{{c}^{2}-{a}^{2}}$,继而可得∠A的度数.
解答 解:(1)∵在Rt△ABC中,c=8$\sqrt{3}$,∠A=60°,
∴a=csinA=8$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=12;
b=ccosA=8$\sqrt{3}$×$\frac{1}{2}$=4$\sqrt{3}$;
(2)∵在Rt△ABC中,c=$\sqrt{6}$,a=$\sqrt{4}$,
∴sinA=$\frac{a}{c}$=$\frac{\sqrt{4}}{\sqrt{6}}$=$\frac{\sqrt{6}}{3}$,
b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{2}$,
∴∠A≈54.74°.
点评 本题主要考查解直角三角形,熟练掌握解直角三角形的依据是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
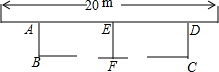 如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.若两个鸡场总面积为96m2,求x.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.若两个鸡场总面积为96m2,求x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:在△ABC中,DE∥BC,交AB于D,交AC于E,且AB=16cm,AC=12cm,BC=20cm.
如图:在△ABC中,DE∥BC,交AB于D,交AC于E,且AB=16cm,AC=12cm,BC=20cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com