

分析 (1)分点P在ON和MN上两种情况用面积公式求解即可;
(2)利用角平分线定理即可求出点P的坐标,进而得出OP;
(3)分三种情况利用等腰三角形的性质和直角三角形的性质,勾股定理即可得出点B的坐标.
解答 解:(1)如图1,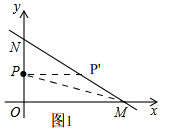
在Rt△MON中,ON=6cm,∠OMN=30°,
∴OM=6$\sqrt{3}$,MN=12,
设△OPM的边OM上的高为h,
∴S=S△POM=$\frac{1}{2}$OM×h=3$\sqrt{3}$h=9$\sqrt{3}$,
∴h=3,
①当点P在ON上时,2t=3,
∴t=$\frac{3}{2}$,
②∵h=3,ON=6,
∴NP'=$\frac{1}{2}$MN=6,
∴NP+NP'=12,
∴2t=12,
∴t=6,
∴当S=9$\sqrt{3}$cm2时,点P运动的时间t为$\frac{3}{2}$秒或6秒;
(2)设P(0,n),
∴OP=n,PN=6-n,
∵MP平分∠OMN,
∴$\frac{OM}{MN}=\frac{OP}{PN}$,
∴$\frac{6\sqrt{3}}{12}=\frac{n}{6-n}$,
∴n=12$\sqrt{3}$-18;
∴OP=12$\sqrt{3}$-18,
(3)∵△EFB为等腰三角形,
∴①当BE=EF时,如图3,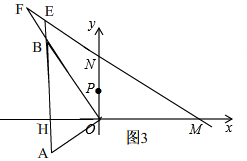
∴∠EFB=30°,
∴α=∠BOM=180°-∠OMH-∠OFM=120°,
∴∠HOF=60°,
∴∠AOH=30°,
∵∠ABO=60°,
∴∠BHO=90°,
∴BH⊥OM,
在Rt△OBH中,OB=6$\sqrt{3}$,∠OBH=30°,
∴OH=$\frac{1}{2}$OB=3$\sqrt{3}$,BH=$\sqrt{3}$OH=9,
∴B(-3$\sqrt{3}$,9);
②当BF=EF时,∴∠BEF=∠B=30°,
∴∠BFE=120°,
∴α=∠BOM=180°-∠OMH-∠OFM=30°,
∴AB∥OM,
如图4,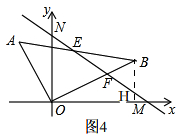
过点B作BH⊥OM,
由旋转得,OB=OM=6$\sqrt{3}$,
在Rt△OBH中,∠BOM=30°,
∴BM=3$\sqrt{3}$,OM=9,
∴B(9,3$\sqrt{3}$);
③当BE=BF时,∴∠BEF=∠BFE=$\frac{1}{2}$(180°-30°)=75°,
∴α=∠BOM=180°-∠OMB-∠OFM=75°,
∴MF=OM=6$\sqrt{3}$,
如图2,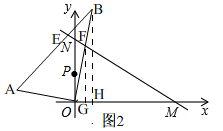
过点B作BH⊥OM.过点F作FG⊥OM,
∴FG∥BH,
∴$\frac{OF}{OB}=\frac{FG}{OB}$,
∴α=∠BOM=180°-∠OMN-∠OFM=75°,
在Rt△FGM中,∠OMN=30°,
∴FG=3$\sqrt{3}$,MG=9,
∴OG=OM-MG=6$\sqrt{3}$-9,
在Rt△OFG中,tan∠OFG=$\frac{OG}{FG}$=2-$\sqrt{3}$=tan∠OBH=$\frac{OH}{BH}$,
∴OH=(2-$\sqrt{3}$)BH,
在Rt△OBH中,OB=6$\sqrt{3}$,
∴根据勾股定理得,OH2+BH2=OB2,
∴[(2-$\sqrt{3}$)BH]2+BH2=108,
∴BH=3$\sqrt{6-3\sqrt{3}}$=3×$\frac{3\sqrt{2}-\sqrt{6}}{2}$=$\frac{9\sqrt{2}-3\sqrt{6}}{2}$,
∴OH=$\frac{27\sqrt{2}-15\sqrt{6}}{2}$,
∴B($\frac{27\sqrt{2}-15\sqrt{6}}{2}$,$\frac{9\sqrt{2}-3\sqrt{6}}{2}$),
点评 此题是几何变换综合题,主要考查了三角形的面积公式,角平分线定理,等腰三角形的性质,直角三角形的性质,勾股定理,解本题的关键是分类讨论,也是解本题的难点,计算量比较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若ac=bc,则a=b | B. | 若a2=b2,则a=b | C. | 若a+b=b+a,则a=b | D. | 若$\frac{a}{c}=\frac{b}{c}$,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
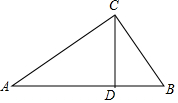 如图,CD是Rt△ABC斜边AB上的高,则下列等式不成立的是( )
如图,CD是Rt△ABC斜边AB上的高,则下列等式不成立的是( )| A. | sinA=$\frac{CD}{AC}$ | B. | sinA=$\frac{BC}{AB}$ | C. | sinA=$\frac{BD}{BC}$ | D. | sinA=$\frac{AD}{AC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com