【题目】已知：直线AB与直线CD相交于点O，∠BOC=45°，
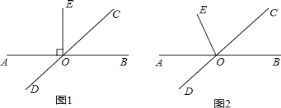
（1）如图1，若EO⊥AB，求∠DOE的度数；
（2）如图2，若EO平分∠AOC，求∠DOE的度数．
【答案】（1）135°；（2）112.5°
【解析】
试题分析：（1）根据对顶角相等求∠AOD，由垂直的性质求∠AOE，根据∠DOE=∠AOD+∠AOE求解；
（2）由邻补角的性质求∠AOC，根据EO平分∠AOC求∠AOE，再由∠DOE=∠AOD+∠AOE求解．
解：（1）∵直线AB与直线CD相交，
∴∠AOD=∠BOC=45°．
∵EO⊥AB，
∴∠AOE=90°，
∴∠DOE=∠AOD+∠AOE=135°；
（2）∵直线AB与直线CD相交，
∴∠AOD=∠BOC=45°，∠AOC=135°，
∵EO平分∠AOC，
∴∠AOE=
∠AOC=67.5°，
∴∠DOE=∠AOD+∠AOE=112.5°．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】我市某草莓种植农户喜获丰收，共收获草莓2000kg．经市场调查，可采用批发、零售两种销售方式，这两种销售方式每kg草莓的利润如下表：
销售方式 | 批发 | 零售 |
利润（元/kg） | 6 | 12 |
设按计划全部售出后的总利润为y元，其中批发量为xkg．
（1）求y与x之间的函数关系式；
（2）若零售量不超过批发量的4倍，求该农户按计划全部售完后获得的最大利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA2=4，则△AnBnAn+1的边长为 ．
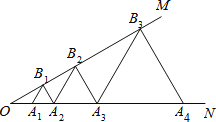
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（ ）
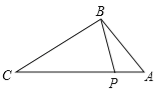
A. ∠ABP=∠C B. ∠APB=∠ABC C. 
=
D. 
=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】[背景知识]数轴是初中数学的一个重要工具，利用数轴可以将数与形完美的结合．研究数轴我们发现了许多重要的规律：数轴上A点、B点表示的数为a、b，则A，B两点之间的距离AB=|a﹣b|，若a＞b，则可简化为AB=a﹣b；线段AB的中点M表示的数为
．
[问题情境]
已知数轴上有A、B两点，分别表示的数为﹣10，8，点A以每秒3个单位的速度沿数轴向右匀速运动，点B以每秒2个单位向左匀速运动．设运动时间为t秒（t＞0）．
[综合运用]
（1）运动开始前，A、B两点的距离为 ；线段AB的中点M所表示的数 ．
（2）点A运动t秒后所在位置的点表示的数为 ；点B运动t秒后所在位置的点表示的数为 ；（用含t的代数式表示）
（3）它们按上述方式运动，A、B两点经过多少秒会相遇，相遇点所表示的数是什么？
（4）若A，B按上述方式继续运动下去，线段AB的中点M能否与原点重合？若能，求出运动时间，并直接写出中点M的运动方向和运动速度；若不能，请说明理由．（当A，B两点重合，则中点M也与A，B两点重合）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“丰收1号“小麦的试验田是边长为am（a＞1）的正方形去掉一个边长为1m的正方蓄水池后余下的部分，“丰收2号”小麦的试验田是边长为（a﹣1）m的正方形，两块试验田的小麦都收获了500kg，试说明哪种小麦的单位面积产量高．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法不正确的是（ ）
A. 三角形的一个外角等于两个内角的和 B. 三角形具有稳定性
C. 四边形的内角和与外角和相等 D. 角是轴对称图形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a＞0）与x轴交于点O、M．对称轴为直线x=2，以OM为直径作圆A，以OM的长为边长作菱形ABCD，且点B、C在第四象限，点C在抛物线对称轴上，点D在y轴负半轴上；
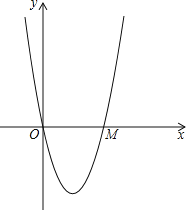
（1）求证：4a+b=0；
（2）若圆A与线段AB的交点为E，试判断直线DE与圆A的位置关系，并说明你的理由；
（3）若抛物线顶点P在菱形ABCD的内部且∠OPM为锐角时，求a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com