
����Ŀ������ij��ݮ��ֲũ��ϲ����գ����ջ��ݮ2000kg�����г����飬�ɲ��������������������۷�ʽ�����������۷�ʽÿkg��ݮ���������±���
���۷�ʽ | ���� | ���� |
����Ԫ/kg�� | 6 | 12 |
�谴�ƻ�ȫ���۳����������ΪyԪ������������Ϊxkg��
��1����y��x֮��ĺ�����ϵʽ��
��2������������������������4�������ũ�����ƻ�ȫ��������õ����������
���𰸡���1��y=6x+12��2000-x����2���������Ϊ21600Ԫ��
��������
�����������1������������=ÿǧ��������ǧ�����г���������ʽ���ɣ�
��2�������������x��ȡֵ��Χ������һ�κ�����������ô𰸼�����
�����������1���������֪������Ϊ��2000-x���֣�
��y=6x+12��2000-x��
������y��x֮��ĺ�����ϵʽΪy=-6x+24000��
��2��������� ��ã�400��x��2000��
��ã�400��x��2000��
��-6��0��
��y��x�����������
����x=400ʱ��y�����ֵ����y���=21600Ԫ��
���������Ϊ21600Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��뾶Ϊ1����A��Բ��������ԭ��O�غϣ��߶�BC�Ķ˵�ֱ���x����y���ϣ���B������Ϊ��6��0������sin��OCB=![]() ��
��
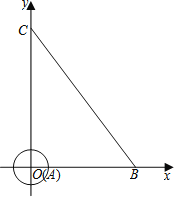
��1������Q���߶�BC��һ�㣬�ҵ�Q�ĺ�����Ϊm��
�����Q�������ꣻ���ú�m�Ĵ���ʽ��ʾ��
������P����A��һ���㣬��PQ����Сֵ��
��2������A��ԭ��O��������1����λ/����ٶ�������OBC�˶�������C�˶�ֹͣ����A���ŵ�A���˶����ƶ���
�ٵ�A��O��B���˶��Ĺ����У�����A��ֱ��BC���У���t��ֵ��
������A�����˶������У�����A���߶�BC������������ʱ��ֱ��д��t�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB=����30�㣼����45�㣩����AOB�����Ϊ��AOC����AOB�IJ���Ϊ��BOD��OMƽ����AOC��ONƽ����BOD��
��1����ͼ������=40�㣬������OM����AOB���ⲿʱ����ֱ�ߡ���������������OD��ON��ȷλ�ã�
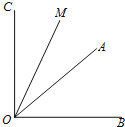
��2����1������MON�Ķ�����Ҫ��д��������̣�
��3��������OM����AOB���ڲ�ʱ���ú����Ĵ���ʽ��ʾ��MON�Ķ�������ֱ��д��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������жϣ����������ϣ�ԭ�����Ե�����������ʾ�������ǻ�Ϊ�෴�������κ������ض��������ĵ�������5ab��![]() ��
��![]() ������ʽ����x2��xy+y2�ǰ���ĸy���������еĶ���ʽ�������ж���ȷ���ǣ� ��
������ʽ����x2��xy+y2�ǰ���ĸy���������еĶ���ʽ�������ж���ȷ���ǣ� ��
A���٢� B���ڢ� C���ۢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��6x+k=0��
��1������������ʵ����ʱ����k�ķ�Χ��
��2����k=��11ʱ�����跽��������x1��x2����x12+x22+8��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A��û����С�������� B��0��������Ҳ�Ǹ���
C������ֻ���������������� D����1�����ĸ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��һ������Գ�ͼ�ε��ǣ� ��
A��ֱ�������� B��ƽ���ı��� C��ֱ������ D��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����x=��
x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����x=��![]() �Ҿ���A��C���㣬��x�����һ����Ϊ��B��
�Ҿ���A��C���㣬��x�����һ����Ϊ��B��

��1����ֱ��д����B�����ꣻ���������߽���ʽ��
��2������PΪֱ��AC�Ϸ����������ϵ�һ�㣬����PA��PC������PAC����������ֵ���������ʱ��P�����꣮
��3�����������Ƿ���ڵ�M������M��MN��ֱx���ڵ�N��ʹ���Ե�A��M��NΪ���������������ABC���ƣ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��AB��ֱ��CD�ཻ�ڵ�O����BOC=45����
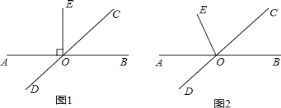
��1����ͼ1����EO��AB������DOE�Ķ�����
��2����ͼ2����EOƽ����AOC������DOE�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com