
【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
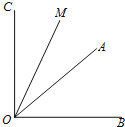
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
【答案】(1)见解析;(2)∠MON=135°或5°;(3)∠MON=α+45°或135°﹣2α.
【解析】
试题分析:(1)分射线OA在∠BOD的外部和内部两种情况作出图形;
(2)根据互为余角和补角的定义求出∠AOC和∠BOD的度数,再根据角平分线的定义可得∠MOA=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,然后根据图形,分∠MON=∠MOA+∠AOB+∠BON和∠MON=∠NOB﹣∠MOA﹣∠AOB分别代入数据进行计算即可得解;
∠BOD,然后根据图形,分∠MON=∠MOA+∠AOB+∠BON和∠MON=∠NOB﹣∠MOA﹣∠AOB分别代入数据进行计算即可得解;
(3)分射线OA在∠BOD的外部和内部两种情况解答.
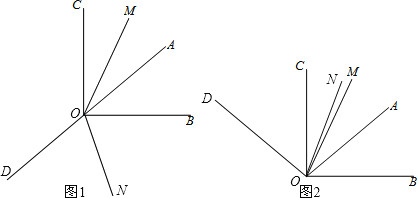
解:(1)如图1,图2所示;
(2)∵∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,
∴∠AOC=90°﹣∠AOB=50°,∠BOD=180°﹣∠AOB=140°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOA=![]() ∠AOC=
∠AOC=![]() ×50°=25°,∠BON=
×50°=25°,∠BON=![]() ∠BOD=
∠BOD=![]() ×140°=70°,
×140°=70°,
①如图1,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°,
②如图2,∠MON=∠NOB﹣∠MOA﹣∠AOB=70°﹣25°﹣40°=5°,
∴∠MON=135°或5°;
(3)∠MON=α+45°或135°﹣2α.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】①三角形的三条角平分线交于一点,这点到三条边的距离相等;②三角形的三条中线交于一点;③三角形的三条高线所在的直线交于一点;④三角形的三条边的垂直平分线交于一点,这点到三个顶点的距离相等.以上说法中正确的是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中,放有三个标号分别为1,2,3的质地、大小都相同的小球.任意摸出一个小球,记为x,再从剩余的球中任意摸出一个小球,又记为y,得到点(x,y).
(1)用画树状图或列表等方法求出点(x,y)的所有可能情况;
(2)求点(x,y)在二次函数y=ax2﹣4ax+c(a≠0)图象的对称轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
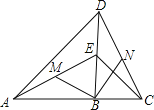
【题目】如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是 (只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:
销售方式 | 批发 | 零售 |
利润(元/kg) | 6 | 12 |
设按计划全部售出后的总利润为y元,其中批发量为xkg.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com