
分析 设甲乙两地的距离为x里,从乙到甲所用的时间是y小时.根据“沿着同一条路从乙地返回甲地,这次步行和骑车走了同样多的时间,结果返回时比去时少用了40分钟”、“从甲地到乙地步行和骑车走了同样长的路程”列出方程组并解答.
解答 解:设甲乙两地的距离为x里,从乙到甲所用的时间是y小时.
根据题意,$\left\{\begin{array}{l}{\frac{\frac{x}{2}}{10}+\frac{\frac{x}{2}}{30}=y+\frac{40}{60}}\\{10×\frac{y}{2}+30×\frac{y}{2}=x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=40}\\{y=2}\end{array}\right.$.
答:甲乙两地的距离为40里,从乙到甲用了2小时.
点评 本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
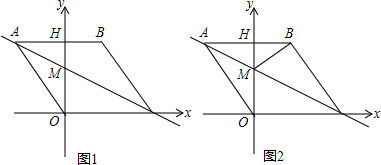
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
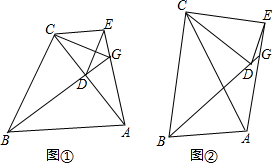
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com