
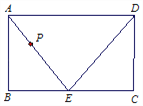
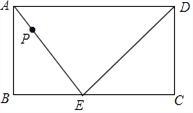
【题目】如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.
(1)若AB=6厘米,BE=8厘米,当点P在线段AE上时,求y关于x的函数表达式;
(2)已知点E是BC的中点,当点P在线段ED和AD上时,求y关于x的函数表达式.

【答案】(1)![]() (0<x≤5);(2)当0<x≤5时,
(0<x≤5);(2)当0<x≤5时, ![]() ;当5<x≤8时,y=32﹣4x.
;当5<x≤8时,y=32﹣4x.
【解析】试题分析:(1)AB已知,利用等面积求出P点到AB的距离,三角形面积公式列式,注意求定义域.(2)利用面积求函数关系,因为P点在两条直线上运动,所以函数是一个分段函数,求出在边界点的值,找出函数定义域.
试题解析:
(1)∵四边形ABCD是矩形,∴∠ABE=90°.
又 AB=8,BE=6,
∴AE=![]() =10,设△ABE中,边AE上的高为h,∵S△ABE=
=10,设△ABE中,边AE上的高为h,∵S△ABE= ![]() AEh=
AEh= ![]() ABBE,∴h=
ABBE,∴h= ![]() ,又 AP=2x,∴
,又 AP=2x,∴![]() (0<x≤5).
(0<x≤5).
(2)∵四边形ABCD是矩形,∴∠B=∠C=90°,AB=DC,AD=BC,
∵E为BC中点,
∴BE=EC,∴△ABE≌△DCE,∴AE=DE,当点P运动至点D时,S△ABP=S△ABD,
由题意得![]() x=32﹣4x,解得x=5,
x=32﹣4x,解得x=5,
当点P运动一周回到点A时,S△ABP=0,由题意得32﹣4x=0,解得x=8,
∴AD=2×(8﹣5)=6,∴BC=6,∴BE=3,且AE+ED=2×5=10,
∴AE=5,在Rt△ABE中,AB= ![]() =4,设△ABE中,边AE上的高为h,
=4,设△ABE中,边AE上的高为h,
∵S△ABE= ![]() AEh=
AEh= ![]() ABBE,∴h=
ABBE,∴h= ![]() ,又 AP=2x,
,又 AP=2x,
∴当点P从A运动至点D时,y= ![]() x(0<x≤2.5),
x(0<x≤2.5),
∴y关于x的函数表达式为:当0<x≤5时, ![]()


科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
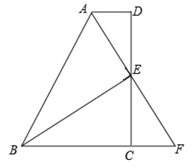
【题目】如图,在四边形 ABCD 中,AD∥BC,E 为 CD 的中点,连接 AE、BE,延长 AE 交 BC 的 延长线于点 F.
(1)△DAE 和△CFE 全等吗?说明理由;
(2)若 AB=BC+AD,说明 BE⊥AF;
(3)在(2)的条件下,若 EF=6,CE=5,∠D=90°,你能否求出 E 到 AB 的距离?如果能 请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() )0+(-
)0+(-![]() )﹣2
)﹣2
(2)利用乘法公式计算:898×902+4
(3)(3x﹣2y)(﹣3x﹣2y)﹣(4y﹣x)
(4)(a+2b﹣3c)(a﹣2b+3c)
(5)先化简,再求值:[(a+4)2﹣(3a﹣2)a﹣8]+(2a),其中a=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+4m(m>0)的图象经过点B(p,2m),其中m>0.
(1)若m=1,且k=﹣1,求点B的坐标;
(2)已知点A(m,0),若直线y=kx+4m与x轴交于点C(n,0),n+2p=4m,试判断线段AB上是否存在一点N,使得点N到坐标原点O与到点C的距离之和等于线段OB的长,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22019的值,可令S=1+2+22+23+…+22019,则2S=2+22+23+…+22019+22020因此2S-S=22020-1.仿照以上推理,计算出1+5+52+53+…+52019的值为( )
A. 52019-1B. 52020-1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为平面直角坐标系的原点,在矩形
为平面直角坐标系的原点,在矩形![]() 中,两边
中,两边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,且点
轴上,且点![]() 满足:
满足:![]() .
.


(1)求点![]() 的坐标(___,_____);
的坐标(___,_____);
(2)若过点![]() 的直线
的直线![]() 与矩形
与矩形![]() 的
的![]() 边交于点
边交于点![]() ,且将矩形
,且将矩形![]() 的面积分为
的面积分为![]() 两部分,
两部分,
①求直线![]() 的解析式;
的解析式;
②在直线![]() 确定一点
确定一点![]() ,使得
,使得![]() 的面积等于矩形
的面积等于矩形![]() 的面积,求点
的面积,求点![]() 的坐标;
的坐标;
(3)![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 在坐标轴上,
在坐标轴上,![]() 为(2)中直线
为(2)中直线![]() 上一动点,若四点
上一动点,若四点![]() 、
、![]() 、
、![]() 、
、![]() 构成平行四边形,直接写出
构成平行四边形,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
(1)当BG=2,DH=3时,则GH:HF= ,∠AGH= °;
(2)若BG=3,DH=1,求DF、EG的长;
(3)设BG=x,DH=y,若△ABG∽△FDH,求y与x之间的函数关系式,并求出y的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com