

分析 (1)首先将A点代入,进而求出函数解析式进而利用配方法求出顶点坐标;
(2)首先设M(m,m2-2m-3),G(m,m-3),则GM=m-3-m2+2m+3=-m2+3m,再利用S△BCM=$\frac{1}{2}$GM(BN+ON)=$\frac{1}{2}$GM•OB求出答案;
(3)首先得出△AOC∽△DCB,进而得出∠E=∠OCB=45°,则tan∠E=1.
解答 解:(1)将(-1,0)代入y=x2-2x+c,
则1+2+c=0,解得:c=-3,
∴y=x2-2x-3
=x2-2x+1-4
=(x-1)2-4
∴D(1,-4);
(2)令y=0,则x2-2x-3=0,
解得:x1=3,x2=-1,
∴B(3,0),C(0,3),
∴yBC=x-3,
如图(1),过M作NM⊥x轴交AB于N,交BC于G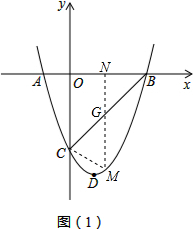
设M(m,m2-2m-3),G(m,m-3),
∴GM=m-3-m2+2m+3
=-m2+3m
∴S△BCM=$\frac{1}{2}$GM(BN+ON)=$\frac{1}{2}$GM•OB
=$\frac{1}{2}$×(-m2+3m)×3
=-$\frac{3}{2}$(m2-3m+$\frac{9}{4}$-$\frac{9}{4}$)
=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$
当m=$\frac{3}{2}$时,m2-2m-3=$\frac{9}{4}$-2×$\frac{3}{2}$-3=-$\frac{15}{4}$
∴G($\frac{3}{2}$,-$\frac{15}{4}$),面积最大值是$\frac{27}{8}$;
(3)如图(2),连接CD,过D作DG⊥x轴于G,DF⊥y轴于F,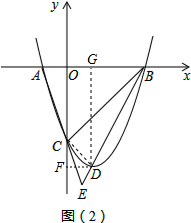
由C(0,-3),B(3,0),D(1,-4),有
CF=FD=1,OC=OB=3,
∴∠OCB=∠FCD=45°,
∴∠BCD=∠AOC=90°,
∵$\frac{AO}{OC}$=$\frac{CD}{BC}$=$\frac{1}{3}$,
∴△AOC∽△DCB,
∴∠ACO=∠CBD,
∵∠ACB=∠ACO+∠OCB=∠CBD+∠E,
∴∠E=∠OCB=45°,
∴tan∠E=1.
点评 此题主要考查了配方法求二次函数顶点坐标以及三角形面积求法和相似三角形的判定与性质等知识,正确表示出△BCM的面积是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
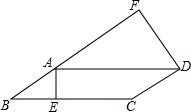 已知,如图,在?ABCD中,AE⊥BC,DF⊥BA垂足分别是E、F,若AB=3,BC=6,AE=2,则DF=4,AF=2$\sqrt{5}$.
已知,如图,在?ABCD中,AE⊥BC,DF⊥BA垂足分别是E、F,若AB=3,BC=6,AE=2,则DF=4,AF=2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
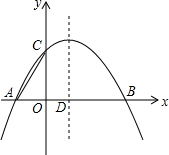 已知二次函数y=ax2+bx+c的图象经过A(-2,0)、B(4,0)、C(O,3)三点,连接AC,该二次函数图象的对称轴与x轴相交于点D.
已知二次函数y=ax2+bx+c的图象经过A(-2,0)、B(4,0)、C(O,3)三点,连接AC,该二次函数图象的对称轴与x轴相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}x-a$分别与x轴、y轴相交于B、C两点,并且与直线MA相交于N点.
已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}x-a$分别与x轴、y轴相交于B、C两点,并且与直线MA相交于N点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com