
 如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.
如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.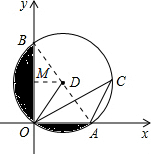 解:(1)连接AB,
解:(1)连接AB,| 3 |
| nπr2 |
| 360 |
| 120×π×16 |
| 360 |
| 16π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| nπr2 |
| 360 |
| 60×π×16 |
| 360 |
| 8π |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 16π |
| 3 |
| 8π |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.
如图,在梯形ABCD中,AD∥BC,AE=EG=GB,DF=FH=HC.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、打开电视机,正在播放新闻 |
| B、在同一年出生的367名学生中,至少有两人的生日是同一天 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com