考点:圆的综合题
专题:
分析:(1)设直线与圆相切于点M,连接O1M,则O1M⊥l,过点O1作直线NH⊥x轴,与l交于点N,与x轴交于点H,因为直线的k=1,所以直线与x轴的夹角等于45°,△OMN是等腰直角三角形,点N的坐标即可表示出来,再把点N的坐标代入直线解析式,即可求出b值;
(2)利用反比例函数图象关于直线y=x对称,作直线y=x的图象与圆有两交点,根据直线与x轴的夹角是45°,用圆的半径表示出两个交点坐标,分别代入反比例函数表达式求出k的值,k的取值就在这两个数值之间.
解答:解:(1)如图,根据题意可知⊙O
1与x轴,y轴分别相切,
设直线l与⊙O
1相切于点M,
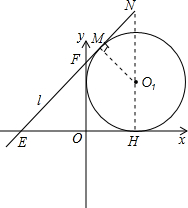
则O
1M⊥l,过点O
1作直线NH⊥x轴,与l交于点N,与x轴交于点H,
又∵直线l与x轴,y轴分别交于点E(-b,0),F(0,b),
∴OE=OF=b,
∴∠NEO=45°,
∴∠ENO
1=45°,
∴∠NO
1M=45°,
在Rt△O
1MN中,O
1N=O
1M÷sin45°=
.
∴点N的坐标为N(1,
+1),
把点N坐标代入y=x+b得:
+1=1+b,
解得:b=
.
(2)如图,设经过点O,O
1的直线交⊙O
1于点A,D,则由已知,直线OO
1;
y=x是圆与反比例函数图象的对称轴,当反比例函数y=
的图象与⊙O
1直径AD相交时(点A,D除外),
则反比例函数y=
的图象与⊙O
1有两个点.
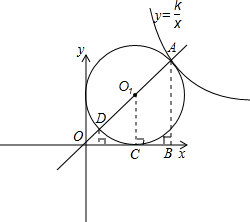
过点A作AB⊥x轴交x轴于点B,过O
1作O
1C⊥x轴于点C,
OO
1=O
1C÷sin45°=1,OA=1+
,
所以OB=AB=OA•sina45°=1+
,
因此点A的坐标是A(1+
,1+
),
将点A坐标代入y=
,
解得:k=
+
,
同理可求得点D的坐标为D(1-
,1-
),
将点D的坐标代入y=
,解得:k=
-
,
所以当反比例函数y=
的图象与⊙O
1有两个交点时,
k的取值范围是:
-
<k<
+
.
点评:本题考查了和圆有关的综合题,其中用到的知识点主要有一次函数图象的性质和反比例函数图象的性质,结合圆的特点直线的k等于1时与x轴的夹角等于45°是解本题的关键,也是解决本题的突破口.





 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案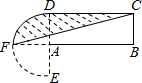 设计一个商标图案,如图6-2阴影部分,其中A为半圆DEF的圆心,BC=a,AB=b.
设计一个商标图案,如图6-2阴影部分,其中A为半圆DEF的圆心,BC=a,AB=b.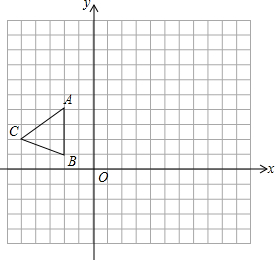 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2). 如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.
如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴,y轴分别交于A,B两点,点A的坐标为(4,0),OC与⊙D相交于点C,∠OCA=30°.