
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
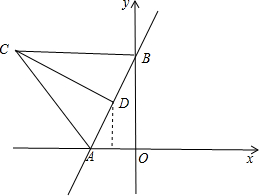 解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-1,0),B点的坐标为(0,
解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-1,0),B点的坐标为(0,| 3 |
| 3 |
| OA2+OB2 |
| ||
| 3 |
| ||
| 3 |
6-2
| ||
| 3 |
| ||
| 3 |
6-2
| ||
| 3 |
| 1 |
| 2 |


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
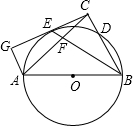 如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.
如图,以△ABC的边AB为直径的⊙PO交BC边于点D,∠ABC的平分线分别于⊙O、AC相交于E、F两点,过A作AG∥BC交CE的延长线于点G,CG⊥BC.| EF |
| BF |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、打开电视机,正在播放新闻 |
| B、在同一年出生的367名学生中,至少有两人的生日是同一天 |
| C、通过长期努力学习,你会成为数学家 |
| D、下雨天,每个人都打着雨伞 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):查看答案和解析>>
科目:初中数学 来源: 题型:
 从这家超市回到家中,圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,
从这家超市回到家中,圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com