
【题目】如图,在长方形ABCD中,AB=6,BC=10,AE=2,连接BE、CE,线段CD上有一点H,将△EDH沿直线EH折叠,折叠后点D落在EC上的点D′处,若D′N⊥AD于点N,与EH交于点M.则①△D′MH与△CBE都是等腰三角形;②∠BEH为直角;③DH长度为![]() ,④
,④![]() ;以上说法正确的个数有( )
;以上说法正确的个数有( )
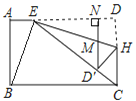
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①根据两直线平行内错角相等和翻折的性质得出两底角相等证的△D′MH是等腰三角形;根据勾股定理算的![]() ,即可证明△CBE都是等腰三角形;②根据翻折性质得出∠D′EH=∠HED,再根据两直线平行同旁内角互补得出2∠BEC+2∠D′EH=180°,最后解得∠BEH为直角;③根据△D′HC∽△DEC得出
,即可证明△CBE都是等腰三角形;②根据翻折性质得出∠D′EH=∠HED,再根据两直线平行同旁内角互补得出2∠BEC+2∠D′EH=180°,最后解得∠BEH为直角;③根据△D′HC∽△DEC得出![]() ,解得D′H,再根据翻折性质得出DH=D′H即可;④过点
,解得D′H,再根据翻折性质得出DH=D′H即可;④过点![]() 做
做![]() ,△ED′M与△EMN是等高三角形,
,△ED′M与△EMN是等高三角形,![]()
再证的△D′MF∽△CH D′,再根据相似三角形的性质即可求解.
①∵D′N⊥AD,长方形ABCD
∴![]()
∴![]()
根据翻折性质可得:![]()
∴![]()
∴△D′MH是等腰三角形
∵在长方形ABCD中,AB=6,BC=10,AE=2
∴![]()
∴![]()
∴![]()
∴△CBE是等腰三角形
故①正确;
②根据翻折性质可得:∠D′EH=∠HED
∵![]()
∴![]()
∴![]() ,则
,则![]()
∴![]()
故②正确;
③根据翻折的性质得:![]()
∴![]()
∴△D′HC∽△DEC
∴![]() ,则
,则![]()
解得:![]()
故③错误;
④过点![]() 做
做![]() ,垂直为F,如图所示:
,垂直为F,如图所示:
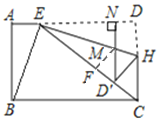
∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]()
根据翻折性质可知![]()
∴![]() 是
是![]() 的角平分线
的角平分线
∴![]()
∵△ED′M与△EMN是等高三角形
∴![]()
故④正确
综上所述:说法正确的有2个.
故选:B.


科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为点P的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)求点A(2,1)的“坐标差”和抛物线y=﹣x2+3x+4的“特征值”.
(2)某二次函数=﹣x2+bx+c(c≠0)的“特征值”为﹣1,点B与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等,求此二次函数的解析式.
(3)如图所示,二次函数y=﹣x2+px+q的图象顶点在“坐标差”为2的一次函数的图象上,四边形DEFO是矩形,点E的坐标为(7,3),点O为坐标原点,点D在x轴上,当二次函数y=﹣x2+px+q的图象与矩形的边有四个交点时,求p的取值范围.
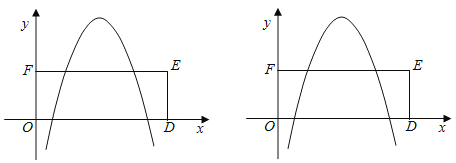
查看答案和解析>>
科目:初中数学 来源: 题型:
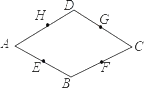
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
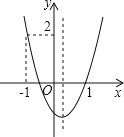
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法,保留作图痕迹)
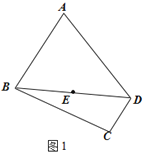
(一)如图1,在四边形ABCD中,CD∥AB,AB=2CD,BD=AD,E为BD中点,请仅用无刻度的直尺在图1中,画出△ABD的AB边上的高线DF.
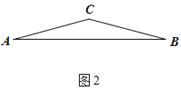
(二)如图2,已知等腰△ABC,∠ACB=150°.
(1)仅用没有无刻度的直尺和圆规作一个△ABD,使∠ADB=75°,∠ABD=60°.
(2)在⑴的前提下,连接CD,若AB=2+2![]() .则CD的长为_______.
.则CD的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车清洗店,清洗一辆汽车定价20元时每天能清洗45辆,定价25元时每天能清洗30辆,假设清洗汽车辆数![]() (辆)与定价
(辆)与定价![]() (元)(
(元)(![]() 取整数)是一次函数关系(清洗每辆汽车成本忽略不计).
取整数)是一次函数关系(清洗每辆汽车成本忽略不计).
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)若清洗一辆汽车定价不低于15元且不超过50元,且该汽车清洗店每天需支付电费、水费和员工工资共计200元,问:定价为多少时,该汽车清洗店每天获利最大?最大获利多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
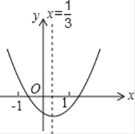
【题目】小明从二次函数y=ax2+bx+c的图象(如图)中观察得到了下面五条信息:①abc>0 ; ②2a﹣3b=0 ; ③b2﹣4ac>0;④a+b+c>0; ⑤4b<c.则其中结论正确的个数是( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com