
【题目】作图题(不写作法,保留作图痕迹)
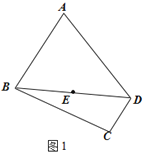
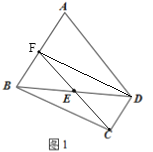
(一)如图1,在四边形ABCD中,CD∥AB,AB=2CD,BD=AD,E为BD中点,请仅用无刻度的直尺在图1中,画出△ABD的AB边上的高线DF.
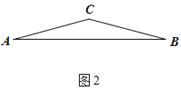
(二)如图2,已知等腰△ABC,∠ACB=150°.
(1)仅用没有无刻度的直尺和圆规作一个△ABD,使∠ADB=75°,∠ABD=60°.
(2)在⑴的前提下,连接CD,若AB=2+2![]() .则CD的长为_______.
.则CD的长为_______.
【答案】(一)见解析;(二)(1)见解析;(2)![]() .
.
【解析】
(一)连接CE交AB于F,连接DF;
(二) (1)以C为圆心,AC为半径画圆C,以B为圆心适当半径画弧,于AB要有交点,再以于AB的交点为圆心同样的半径画弧于刚才的弧交于一点,连接B与两个弧的交点即可得到∠ABD=60°,交圆C于D,连接AD即可得到∠ADB=75°;(2)设半径CD为![]() 先根据特殊角度算出AD、DB含
先根据特殊角度算出AD、DB含![]() 的代数式,再根据余弦定理列出关于
的代数式,再根据余弦定理列出关于![]() 的方程,解得
的方程,解得![]() 即可.
即可.
(一)连接CE交AB于F,连接DF.
(二)(1)以C为圆心,AC为半径画圆C尺规作∠ABD=60°
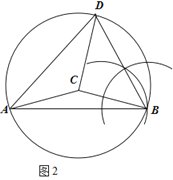
(2)过C点作CE⊥DA垂足为E,如图3所示:

设半径CD为![]()
∵∠ABD=60°
∴∠ACD=120°
∴∠EDC=30°
∴![]()
∵∠ADB=75°,∠ABD=60°
∴∠DAB=45°
∴∠DCB=90°
∴![]()
根据余弦定理得:![]()
代入各值解得:![]()
解得:![]()
即![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
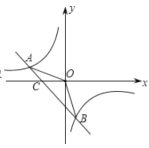
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 和反比例函数
和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 的
的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度.
图1为点P在⊙O外的情形示意图.
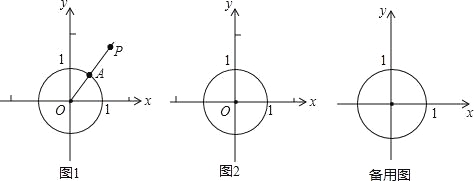
(1)若点B(1,0),C(1,1),D(0,![]() ),则SB= ;SC= ;SD= ;
),则SB= ;SC= ;SD= ;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR,直接写出满足条件的线段PQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( )
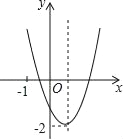
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=6,BC=10,AE=2,连接BE、CE,线段CD上有一点H,将△EDH沿直线EH折叠,折叠后点D落在EC上的点D′处,若D′N⊥AD于点N,与EH交于点M.则①△D′MH与△CBE都是等腰三角形;②∠BEH为直角;③DH长度为![]() ,④
,④![]() ;以上说法正确的个数有( )
;以上说法正确的个数有( )
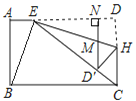
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是( )

A.18m2B.![]() m2C.
m2C.![]() m2D.
m2D.![]() m2
m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(3,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C,延长C1B1交x轴于点A2;作第3个正方形A2B2C2C1,…按这样的规律进行下去,第5个正方形的边长为_____.
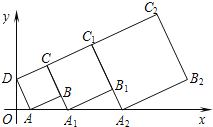
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
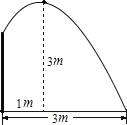
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种成本为![]() 元
元![]() 的水产品,若按
的水产品,若按![]() 元
元![]() 销售,一个月可售出
销售,一个月可售出![]() ,售价毎涨
,售价毎涨![]() 元,月销售量就减少
元,月销售量就减少![]() .
.
![]() 写出月销售利润
写出月销售利润![]() (元)与售价
(元)与售价![]() (元
(元![]() )之间的函数表达式;
)之间的函数表达式;
![]() 当售价定为多少元时,该商店月销售利润为
当售价定为多少元时,该商店月销售利润为![]() 元?
元?
![]() 当售价定为多少元时会获得最大利润?求出最大利润.
当售价定为多少元时会获得最大利润?求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com