
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
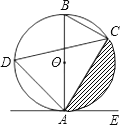
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求阴影部分的面积.
【答案】(1)60°;(2)见解析;(3)![]()
【解析】
(1)根据∠ABC与∠D都是劣弧AC所对的圆周角,利用圆周角定理可证出∠ABC=∠D=60°;
(2)根据AB是⊙O的直径,利用直径所对的圆周角是直角得到∠ACB=90°,结合∠ABC=60°求得∠BAC=30°,从而推出∠BAE=90°,即OA⊥AE,可得AE是⊙O的切线;
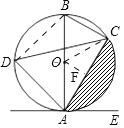
(3)连接OC,作OF⊥AC,根据三角形中位线性质得出OF=2,根据圆周角定理得出∠AOC=120°,然后根据S阴影=S扇形﹣S△AOC即可求得.
解:(1)∵∠ABC与∠D都是劣弧AC所对的圆周角,∠D=60°,
∴∠ABC=∠D=60°;
(2)∵AB是⊙O的直径,∴∠ACB=90°.
可得∠BAC=90°﹣∠ABC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,得OA⊥AE,
又∵OA是⊙O的半径,
∴AE是⊙O的切线;
(3)连接OC,作OF⊥AC,
∴OF垂直平分AC,
∵OA=OB,
∴OF=![]() BC=2,
BC=2,
∵∠D=60°,
∴∠AOC=120°,∠ABC=60°,
∴AC=![]() AB=4
AB=4![]() ,
,
∴S阴影=S扇形﹣S△AOC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
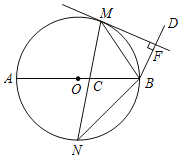
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
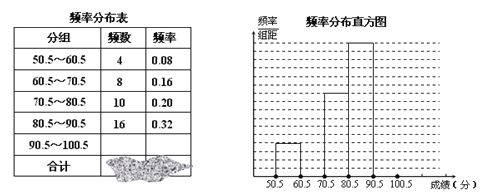
【题目】为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答: .
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答: .
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
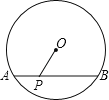
A.4个B.5个C.6个D.7个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的![]() 名领操员进行比赛,成绩如下表:
名领操员进行比赛,成绩如下表:
成绩(分) |
|
|
|
|
人数(人) |
|
|
|
|
(1)这组数据的众数是______,中位数是_______;
(2)已知获得![]() 分的选手中,七、八、九年级分别有
分的选手中,七、八、九年级分别有![]() 人、
人、![]() 人、
人、![]() 人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学图书室计划购买了甲、乙两种故事书.若购买7本甲种故事书和4本乙种故事书需510元;购买3本甲种故事书和5本乙种故事书需350元.
(1)求甲种故事书和乙种故事书的单价;
(2)学校准备购买甲、乙两种故事书共200本,且甲种故事书的数量不少于乙种故事书的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中直线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,点
两点,点![]() 坐标为
坐标为![]() .点
.点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交抛物线于点
,交抛物线于点![]() .
.

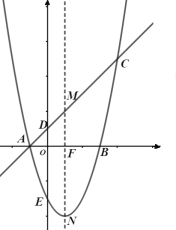
(1)求抛物线的解析式;
(2)是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,如果有,求点
为顶点的四边形为平行四边形,如果有,求点![]() 的坐标,如果没有,请说明理由;
的坐标,如果没有,请说明理由;
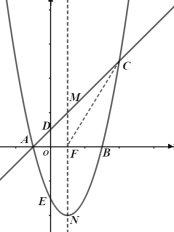
(3)若点![]() 在线段
在线段![]() 上移动时(不含端点),连接
上移动时(不含端点),连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com