
| 每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
| 每天销量(千克) | 50 | 52 | 54 | 56 | … | 86 |
分析 (1)根据图表易知:每千克的售价每下降1元,就能多销售2千克,可据此列出y、x的函数关系式;
(2)已知了销售单价,即可得下调的价格数即x的值,然后代入y、x的函数关系式中,即可得销售数量,进而可根据:每千克的获利额×销售数量=总的获利额,求解即可.
(3)在(2)中已求得了y=66千克,若每天售价不低于30元/kg,那么每天最多销售66千克,设出每次进货最多只能是a千克,那么销售完这些货物最少要用$\frac{a}{66}$天,而凤梨的实际销售时间为:(30-7),可据此列不等式求出a的最大值.
解答 解:(1)由表知:销售单价每下调1元,销售数量增加2kg,故y=50+2x;
(2)当售价为30元/kg时,x=38-30=8,
销售数量为:y=50+2x=66,
则这天的销售利润为:66×(30-20)=660(元).
(3)设一次进货最多只能是a千克,依题意有:
$\frac{a}{66}$≤30-7,解得a≤1518,
即一次进货最多1518千克.
点评 此题主要考查的是一次函数与一元一次不等式的应用,难度适中,理清题意是解题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
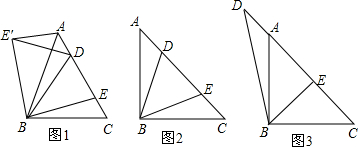
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
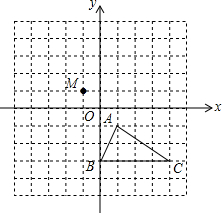 在如图所示的正方形网格中,△ABC的顶点均在格点上,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,点A的坐标为(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0°<α<30° | B. | 30°<α<60° | C. | 60°<α<90° | D. | 45°<α<90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
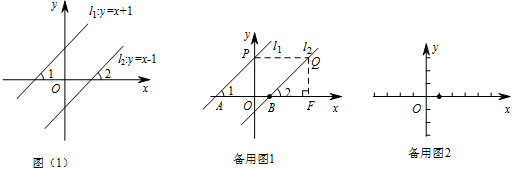
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com