
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÄÚŁŹ”ă![]() ÎȘŚű±êԔ㣏
ÎȘŚű±êԔ㣏![]() ”Ķ„”ă
”Ķ„”ă![]() ÔÚ
ÔÚ![]() ÖáŐę°ëÖᣏ¶„”ă
ÖáŐę°ëÖᣏ¶„”ă![]() Ąą
Ąą![]() ·Ö±đÔÚ
·Ö±đÔÚ![]() Öážș°ëÖáșÍŐę°ëÖáÉÏŁŹ
Öážș°ëÖáșÍŐę°ëÖáÉÏŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]()
Łš1Ł©Çó![]() ”Äł€Łź
”Äł€Łź
Łš2Ł©¶Ż”ă![]() ŽÓ”ă
ŽÓ”ă![]() łö·ąÒÔĂżĂë
łö·ąÒÔĂżĂë![]() žö”„λł€¶È”ÄËÙ¶ÈŃŰ
žö”„λł€¶È”ÄËÙ¶ÈŃŰ![]() ÏòÖŐ”ă
ÏòÖŐ”ă![]() Ô˶ŻŁŹ”ă
Ô˶ŻŁŹ”ă![]() Ô˶Ż”ÄʱŒäÎȘ
Ô˶Ż”ÄʱŒäÎȘ![]() ŁŹÒÔ
ŁŹÒÔ![]() ÎȘб±ßÔÚ
ÎȘб±ßÔÚ![]() ÓÒ±ßÉÏ·œŚś”ÈŃüÖ±œÇÈęœÇĐÎ
ÓÒ±ßÉÏ·œŚś”ÈŃüÖ±œÇÈęœÇĐÎ![]() ŁŹÁŹœÓ
ŁŹÁŹœÓ![]() Ąą
Ąą![]() ŁŹÉè
ŁŹÉè![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() Łš
Łš![]() Ł©ŁŹÇó
Ł©ŁŹÇó![]() Óë
Óë![]() ÖźŒä”ÄșŻÊęčŰϔʜŁŹČąÖ±œÓĐŽłöŚÔ±äÁż
ÖźŒä”ÄșŻÊęčŰϔʜŁŹČąÖ±œÓĐŽłöŚÔ±äÁż![]() ”ÄÈĄÖ”·¶Î§Łź
”ÄÈĄÖ”·¶Î§Łź
Łš3Ł©ÔÚŁš2Ł©”ÄÌőŒțÏÂŁŹčę”ă![]() Śś
Śś![]() ”ÄŽčÏßœ»
”ÄŽčÏßœ»![]() ÖáÓÚ
ÖáÓÚ![]() ŁŹÁŹœÓ
ŁŹÁŹœÓ![]() ŁŹ”±ËıßĐÎ
ŁŹ”±ËıßĐÎ![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() ŁŹÊ±ŁŹÇó
ŁŹÊ±ŁŹÇó![]() ”ÄÖ”Œ°
”ÄÖ”Œ°![]() ”ăŚű±êŁź
”ăŚű±êŁź
ĄŸŽđ°žĄżŁš1Ł©![]() Ł»Łš2Ł©S=2tŁš0ĄÜtĄÜ4Ł©Ł»Łš3Ł©QŁš0ŁŹ-2Ł©Łź
Ł»Łš2Ł©S=2tŁš0ĄÜtĄÜ4Ł©Ł»Łš3Ł©QŁš0ŁŹ-2Ł©Łź
ĄŸœâÎöĄż
Łš1Ł©žùŸĘÈęœÇĐÎĂæ»ęč«ÊœÇó”ĂBC”Äł€ŁŹÈ»șóžùŸĘ”ÈŃüÈęœÇĐΔÄĐÔÖÊÇóOB”Äł€ŁŹŽÓ¶űÀûÓĂčŽčɶšÀíÇóœâŁ»
Łš2Ł©ŚśPMĄÍBCÓÚNŁŹDHĄÍPCÓÚHŁźÀûÓĂčŽčɶšÀíÇółöPC”Äł€ŁšÓĂt±íÊŸŁ©ŒŽżÉœâŸöÎÊÌ⣻
Łš3Ł©ŚśPNĄÍyÖáÓÚNŁŹDKĄÍPNÓÚKŁŹDHĄÍPCÓÚHŁŹÁŹœÓAHĄąDHŁźÊŚÏÈրÜAĄąPĄąDĄąCËÄ”ăčČÔČŁŹÍÆłöĄÏDAC=ĄÏDPC=45ĄăŁŹĄÏDAO=90ĄăŁŹÓÉĄśPNQĄŐĄśDKPŁŹżÉ”ĂDP=PQ=DCŁŹżÉ”ĂËıßĐÎPQCDÊÇŐę·œĐÎŁŹžùŸĘÌâÒâÁĐłö·œłÌŒŽżÉœâŸöÎÊÌ⣻
œâŁșĄß![]()
ĄàBC=8
ÓÖĄß![]() ”Ķ„”ă
”Ķ„”ă![]() ÔÚ
ÔÚ![]() ÖáŐę°ëÖᣏ¶„”ă
ÖáŐę°ëÖᣏ¶„”ă![]() Ąą
Ąą![]() ·Ö±đÔÚ
·Ö±đÔÚ![]() Öážș°ëÖáșÍŐę°ëÖáÉÏŁŹ
Öážș°ëÖáșÍŐę°ëÖáÉÏŁŹ![]() ŁŹ
ŁŹ
ĄàOB=OC=![]() ŁŹ
ŁŹ
ĄàÔÚRtĄśOABÖĐŁŹ![]()
Łš2Ł©ÈçÍŒ1ÖĐŁŹŚśDMĄÍXÖáÓÚMŁŹPKĄÍDMÓÚKœ»yÖáÓÚNŁŹDHĄÍPCÓÚHŁŹŚśPEĄÍxÖáÓÚEŁŹÁŹœÓAHĄąDHŁź
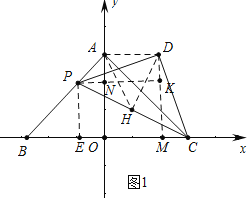
ÓÉŁš1Ł©żÉÖȘŁŹOA=OB=4
ĄàĄÏBAO=ĄÏCAO=45ĄăŁŹŒŽĄÏBAC=90Ąă
Ó֥ߥśPCDÊÇ”ÈŃüÖ±œÇÈęœÇĐÎ
ĄàAH=DH=HP=HCŁŹ
ĄàAĄąPĄąDĄąCËÄ”ăčČÔČŁŹ
ĄàĄÏDAC=ĄÏDPC=45ĄăŁŹ
ĄàĄÏDAO=90ĄăŁŹ
ĄßĄÏDPK+ĄÏPDM=90ĄăŁŹĄÏPDM+ĄÏMDC=90ĄăŁŹ
ĄàĄÏDPK=ĄÏMDCŁŹ
ĄßĄÏPKD=ĄÏDMC=90ĄăŁŹDP=DCŁŹ
ĄàĄśPDKĄŐĄśDCMŁŹ
ĄàPK=DM=OA=4ŁŹ
ĄßOA=OBŁŹĄÏAOB=90ĄăŁŹ
ĄàĄśAOBÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹ
ĄßPEĄÍBCŁŹ
ĄàĄÏPEB=90ĄăŁŹ
ĄàĄÏPBE=ĄÏBPE=45ĄăŁŹ
ĄßPB=![]() tŁŹ
tŁŹ
ÓÉÌâÒâżÉÖȘŁŹËıßĐÎPEONÎȘŸŰĐÎ
ĄàPE=BE=tŁŹON=4-tŁŹ
ĄàCM=DK=AN=OA=ON=OA-PE=4-tŁŹ
ĄàAD=4-Łš4-tŁ©=tŁŹ
ĄàS=![]()
![]() t4=2tŁš0ĄÜtĄÜ4Ł©Łź
t4=2tŁš0ĄÜtĄÜ4Ł©Łź
Łš3Ł©ÈçÍŒ2ÖĐŁŹ
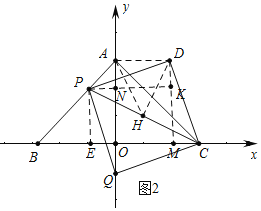
ÓÉŁš2Ł©żÉÖȘŁșPE=BE=tŁŹON=4-tŁŹCE=8-tŁŹ
ÔÚRtĄśPCEÖĐŁŹPC2=t2+Łš8-tŁ©2=2t2-16t+64ŁŹ
ĄßĄśPDCÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹDHĄÍPCŁŹ
ĄàPH=CH=DHŁŹ
ĄàSĄśPDC=![]() =
=![]() Łš0ĄÜtĄÜ4Ł©Łź
Łš0ĄÜtĄÜ4Ł©Łź
ÒŚÖȘAN=PN=DKŁŹĄÏQPN=ĄÏPDKŁŹĄÏPNQ=ĄÏPKD=90ĄăŁŹ
ĄàĄśPNQĄŐĄśDKPŁŹ
ĄàDP=PQ=DCŁŹĄßPQĄÎDCŁŹ
ĄàËıßĐÎPQCDÊÇÆœĐĐËıßĐÎŁŹ
ĄßĄÏDPQ=90ĄăŁŹ
ĄàËıßĐÎPQCDÊÇŸŰĐÎŁŹ
ĄßPD=PQŁŹ
ĄàËıßĐÎPQCDÊÇŐę·œĐÎŁŹ
ÓÉÌâÒâŁș2Łš![]() Ł©=
Ł©=![]() ŁŹ
ŁŹ
2Łš![]() Ł©=10t
Ł©=10t
ŐûÀí”Ăt2-8t+32=0ŁŹ
œâ”ĂŁșt=2»ò16ŁšÉáÆúŁ©ŁŹ
Ąàt=2ʱŁŹËıßĐÎPDCQ”ÄĂæ»ęÎȘ20ŁŹ
ŽËʱPC=2![]() ŁŹPQ=2
ŁŹPQ=2![]() ŁŹPN=2ŁŹON=2ŁŹNQ=
ŁŹPN=2ŁŹON=2ŁŹNQ=![]() =4ŁŹ
=4ŁŹ
ĄàOQ=QN-ON=2ŁŹ
ĄàQŁš0ŁŹ-2Ł©Łź


 Êęѧ°ÂÈüÊîŒÙÌìÌìÁ·ÄÏŸ©Žóѧłö°æÉçÏ”ÁĐŽđ°ž
Êęѧ°ÂÈüÊîŒÙÌìÌìÁ·ÄÏŸ©Žóѧłö°æÉçÏ”ÁĐŽđ°ž ÄÏŽóœÌžšÇÀÏÈÆđĆÜÊîŒÙÏÎœÓœÌłÌÄÏŸ©Žóѧłö°æÉçÏ”ÁĐŽđ°ž
ÄÏŽóœÌžšÇÀÏÈÆđĆÜÊîŒÙÏÎœÓœÌłÌÄÏŸ©Žóѧłö°æÉçÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż¶țŽÎșŻÊę![]() ”ÄÍŒÏóÈçÍŒËùÊŸŁŹÒÔÏÂœáÂÛŁșąÙabcŁŸ0Ł»ąÚ4acŁŒb2Ł»ąÛ2a+bŁŸ0Ł»ąÜÆ䶄”ăŚű±êÎȘŁš
”ÄÍŒÏóÈçÍŒËùÊŸŁŹÒÔÏÂœáÂÛŁșąÙabcŁŸ0Ł»ąÚ4acŁŒb2Ł»ąÛ2a+bŁŸ0Ł»ąÜÆ䶄”ăŚű±êÎȘŁš![]() ŁŹ©2Ł©Ł»ąĘ”±xŁŒ
ŁŹ©2Ł©Ł»ąĘ”±xŁŒ![]() ʱŁŹyËæx”ÄÔöŽó¶űŒőĐĄŁ»ąȚa+b+cŁŸ0ŐęÈ·”ÄÓĐŁšĄĄĄĄŁ©
ʱŁŹyËæx”ÄÔöŽó¶űŒőĐĄŁ»ąȚa+b+cŁŸ0ŐęÈ·”ÄÓĐŁšĄĄĄĄŁ©

A. 3žö B. 4žö C. 5žö D. 6žö
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłÉÌ”êÓĂ1000ÔȘÈËĂń±ÒčșœűËźčûÏúÊÛŁŹčęÁËÒ»¶ÎʱŒäŁŹÓÖÓĂ2400ÔȘÈËĂń±ÒčșœűŐâÖÖËźčûŁŹËùčșÊęÁżÊÇ”ÚÒ»ŽÎčșœűÊęÁż”Ä2±¶ŁŹ”«ĂżÇ§żË”Č۞ń±È”ÚÒ»ŽÎčșœű”ÄčóÁË2ÔȘŁź
Łš1Ł©žĂÉÌ”ê”ÚÒ»ŽÎčșœűËźčû¶àÉÙǧżËŁ»
Łš2Ł©ŒÙÉèžĂÉÌ”êÁœŽÎčșœű”ÄËźčû°ŽÏàÍŹ”ıêŒÛÏúÊÛŁŹŚîșóÊŁÏ”Ä20ǧżË°Ž±êŒÛ”ÄÎćŐÛÓĆ»ĘÏúÊÛŁźÈôÁœŽÎčșœűËźčûÈ«ČżÊÛÍêŁŹÀûÈóČ»”ÍÓÚ950ÔȘŁŹÔòÿǧżËËźčû”ıêŒÛÖÁÉÙÊǶàÉÙÔȘŁż
ŚąŁșÿǧżËËźčû”ÄÏúÊÛÀûÈó”ÈÓÚÿǧżËËźčû”ÄÏúÊی۞ńÓëÿǧżËËźčû”ÄčșœűŒÛžń”ÄČÁœĆúËźčûÈ«ČżÊÛÍê”ÄÀûÈó”ÈÓÚÁœŽÎčșœűËźčû”ÄÏúÊÛÀûÈóÖźșÍŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÙ¶ÁœÌČÄŁșżíÓ변”ıÈÊÇ![]() ŁšÔŒÎȘ
ŁšÔŒÎȘ![]() Ł©”ÄŸŰĐÎœĐŚö»ÆœđŸŰĐÎŁŹ»ÆœđŸŰĐΞűÎÒĂÇÒÔĐ”śĄąÔÈłÆ”ÄĂÀžĐŁźÊÀœçžśčúĐí¶àÖűĂû”ÄœšÖțŁŹÎȘÈĄ”ĂŚîŒŃ”ÄÊÓŸőЧčûŁŹ¶ŒČÉÓĂÁ˻ƜđŸŰĐΔÄÉèŒÆŁŹÏÂĂæÎÒĂÇÓĂżíÎȘ
Ł©”ÄŸŰĐÎœĐŚö»ÆœđŸŰĐÎŁŹ»ÆœđŸŰĐΞűÎÒĂÇÒÔĐ”śĄąÔÈłÆ”ÄĂÀžĐŁźÊÀœçžśčúĐí¶àÖűĂû”ÄœšÖțŁŹÎȘÈĄ”ĂŚîŒŃ”ÄÊÓŸőЧčûŁŹ¶ŒČÉÓĂÁ˻ƜđŸŰĐΔÄÉèŒÆŁŹÏÂĂæÎÒĂÇÓĂżíÎȘ![]() ”ÄŸŰĐÎÖœÆŹŐÛ”ț»ÆœđŸŰĐÎŁšÌáÊŸŁș
”ÄŸŰĐÎÖœÆŹŐÛ”ț»ÆœđŸŰĐÎŁšÌáÊŸŁș![]() Ł©
Ł©
”ÚÒ»ČœŁșÔÚŸŰĐÎÖœÆŹÒ»¶ËÀûÓĂÍŒąÙ”Ä·œ·šŐÛłöÒ»žöŐę·œĐÎŁŹÈ»șó°ŃÖœÆŹŐčÆœŁź

”Ú¶țČœŁșÈçÍŒąÚŁŹ°ŃŐâžöŐę·œĐÎŐÛłÉÁœžöÏà”ȔğŰĐÎŁŹÔÙ°ŃÖœÆŹŐčÆœŁź

”ÚÈęČœŁșŐÛłöÄÚČàŸŰĐΔĶԜÇÏß![]() ŁŹČą°Ń
ŁŹČą°Ń![]() ŐÛ”œÍŒąÛÖĐËùÊŸ”Ä
ŐÛ”œÍŒąÛÖĐËùÊŸ”Ä![]() ŽŠŁź
ŽŠŁź

”ÚËÄČœŁșŐčÆœÖœÆŹŁŹ°ŽŐŐËù”ÔĔă![]() ŐÛłö
ŐÛłö![]() Êč
Êč![]() ÔòÍŒąÜÖĐŸÍ»áłöÏֻƜđŸŰĐÎŁź
ÔòÍŒąÜÖĐŸÍ»áłöÏֻƜđŸŰĐÎŁź

ÎÊÌâœâŸöŁș
Łš1Ł©ÍŒąÛÖĐ![]() _ Łš±ŁÁôžùșĆŁ©Ł»
_ Łš±ŁÁôžùșĆŁ©Ł»
Łš2Ł©ÈçÍŒąÛŁŹĆжÏËıßĐÎ![]() ”ÄĐÎŚŽŁŹČąË”ĂśÀíÓÉŁ»
”ÄĐÎŚŽŁŹČąË”ĂśÀíÓÉŁ»
Łš3Ł©ÇëĐŽłöÍŒąÜÖĐËùÓĐ”Ä»ÆœđŸŰĐÎŁŹČąŃĄÔńÆäÖĐÒ»žö˔ÜÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłÇàŽș”łÖ§ČżÔÚŸ«ŚŒ·öƶ»î¶ŻÖĐŁŹžűœá¶Ô°ï·ö”ÄƶÀ§ŒÒÍ„ÔùËÍŒŚĄąÒÒÁœÖÖÊśĂçÈĂÆäÔÔÖÖŁźÒŃÖȘÒÒÖÖÊśĂç”Č۞ń±ÈŒŚÖÖÊśĂçčó10ÔȘŁŹÓĂ480ÔȘčșÂòÒÒÖÖÊśĂç”ÄżĂÊęÇĄșĂÓëÓĂ360ÔȘčșÂòŒŚÖÖÊśĂç”ÄżĂÊęÏàÍŹŁź
Łš1Ł©ÇóŒŚĄąÒÒÁœÖÖÊśĂçĂżżĂ”Č۞ńžśÊǶàÉÙÔȘŁż
Łš2Ł©ÔÚÊ”ŒÊ°ï·öÖĐŁŹËûĂÇŸö¶šÔÙŽÎčșÂòŒŚĄąÒÒÁœÖÖÊśĂçčČ50żĂŁŹŽËʱŁŹŒŚÖÖÊśĂç”ÄÊی۱ȔÚÒ»ŽÎčșÂòʱœ””ÍÁË10%ŁŹÒÒÖÖÊśĂç”ÄÊÛŒÛČ»±äŁŹÈçčûÔÙŽÎčșÂòÁœÖÖÊśĂç”ÄŚÜ·ŃÓĂČ»łŹčę1500ÔȘŁŹÄÇĂŽËûĂÇŚî¶àżÉčșÂò¶àÉÙżĂÒÒÖÖÊśĂ磿
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłÖĐѧŚé֯ѧÉú”œÉÌłĄČÎŒÓÉç»áÊ”Œù»î¶ŻŁŹËûĂÇČÎÓëÁËÄłÖÖÆ·ĆÆÔ˶ŻĐŹ”ÄÏúÊÛ而śŁŹÒŃÖȘžĂÔ˶ŻĐŹĂżË«”ÄœűŒÛÎȘ120ÔȘŁŹÎȘŃ°ÇóșÏÊÊ”ÄÏúÊی۞ńœűĐĐÁË4Ìì”ÄÊÔÏúŁŹÊÔÏúÇéżöÈç±íËùÊŸŁș

Łš1Ł©čÛČì±íÖĐÊęŸĘŁŹxŁŹyÂúŚăÊČĂŽșŻÊęčŰÏ”ŁżÇëÇółöŐâžöșŻÊęčŰϔʜŁ»
Łš2Ł©ÈôÉÌłĄŒÆ»źĂżÌì”ÄÏúÊÛÀûÈóÎȘ3000ÔȘŁŹÔòÆ䔄ŒÛÓŠ¶šÎȘ¶àÉÙÔȘŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż¶țŽÎșŻÊę![]() ”ÄČż·ÖÍŒÏóÈçÍŒŁŹÍŒÏóčę”ă
”ÄČż·ÖÍŒÏóÈçÍŒŁŹÍŒÏóčę”ă![]() ŁŹ¶ÔłÆÖáÎȘÖ±Ïß
ŁŹ¶ÔłÆÖáÎȘÖ±Ïß![]() ŁŹÏÂÁĐœáÂÛŁșąÙ
ŁŹÏÂÁĐœáÂÛŁșąÙ![]() Ł»ąÚ
Ł»ąÚ![]() Ł»ąÛ
Ł»ąÛ![]() Ł»ąÜ”±
Ł»ąÜ”±![]() ʱŁŹ
ʱŁŹ ![]() ”ÄÖ”Ëæ
”ÄÖ”Ëæ![]() Ö””ÄÔöŽó¶űÔöŽóŁ»ąĘ”±șŻÊęÖ”
Ö””ÄÔöŽó¶űÔöŽóŁ»ąĘ”±șŻÊęÖ”![]() ʱŁŹŚÔ±äÁż
ʱŁŹŚÔ±äÁż![]() ”ÄÈĄÖ”·¶Î§ÊÇ
”ÄÈĄÖ”·¶Î§ÊÇ![]() »ò
»ò![]() ŁźÆäÖĐŐęÈ·”ÄœáÂÛÓĐ__________Łź
ŁźÆäÖĐŐęÈ·”ÄœáÂÛÓĐ__________Łź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĄśABCșÍĄśBDE¶ŒÊǔȱßÈęœÇĐÎŁŹ”ăAŁŹBŁŹDÔÚÒ»ÌőÖ±ÏßÉÏĄŁžűłö4žöœáÂÛŁșąÙAE=CDŁ»ąÚABĄÍFBŁ»ąÛĄÏAFC=60ĄăŁ»ąÜĄśBGHÊǔȱßÈęœÇĐÎĄŁÆäÖĐŐęÈ·”ÄÊÇŁš Ł©
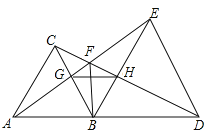
A.ąÙŁŹąÚŁŹąÛB.ąÙŁŹąÚŁŹąÜ
C.ąÙŁŹąÛŁŹąÜD.ąÚŁŹąÛŁŹąÜ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÖŰÇìÊĐÓĐ![]() ÎćžöŸ°ÇűșÜÊÜÓÎżÍÏČ°źŁŹÒ»ÂĂĐĐÉç¶ÔijХÇűŸÓĂńÔÚÊîŒÙÆÚŒäÈ„ÒÔÉÏÎćžöŸ°ÇűÂĂÓÎ(Ö»ŃĄÒ»žöŸ°Çű)”ÄÒâÏòŚöÁËÒ»ŽÎËæ»ú”śČéÍłŒÆŁŹČąžùŸĘŐâžöÍłŒÆœáčûÖÆŚśÁËÈçÏÂÁœ·ùČ»ÍêŐû”ÄÍłŒÆÍŒŁź
ÎćžöŸ°ÇűșÜÊÜÓÎżÍÏČ°źŁŹÒ»ÂĂĐĐÉç¶ÔijХÇűŸÓĂńÔÚÊîŒÙÆÚŒäÈ„ÒÔÉÏÎćžöŸ°ÇűÂĂÓÎ(Ö»ŃĄÒ»žöŸ°Çű)”ÄÒâÏòŚöÁËÒ»ŽÎËæ»ú”śČéÍłŒÆŁŹČąžùŸĘŐâžöÍłŒÆœáčûÖÆŚśÁËÈçÏÂÁœ·ùČ»ÍêŐû”ÄÍłŒÆÍŒŁź

![]() žĂĐĄÇűŸÓĂńÔÚŐâŽÎËæ»ú”śČéÖб»”śČ锜”ÄÈËÊęÊÇ_______ÈËŁŹ
žĂĐĄÇűŸÓĂńÔÚŐâŽÎËæ»ú”śČéÖб»”śČ锜”ÄÈËÊęÊÇ_______ÈËŁŹ ![]() ÏëÈ„
ÏëÈ„![]() Ÿ°Çű”ÄÈËÓĐ_________ÈËŁŹ ČąČčÈ«ÌőĐÎÍłŒÆÍŒŁź
Ÿ°Çű”ÄÈËÓĐ_________ÈËŁŹ ČąČčÈ«ÌőĐÎÍłŒÆÍŒŁź
![]() ±»”śČ锜”ÄŸÓĂńÏëÈ„ Ÿ°ÇűÂĂÓΔÄÈËÊęŚî¶àŁŹÈôžĂĐĄÇűÓĐŸÓĂń
±»”śČ锜”ÄŸÓĂńÏëÈ„ Ÿ°ÇűÂĂÓΔÄÈËÊęŚî¶àŁŹÈôžĂĐĄÇűÓĐŸÓĂń![]() ÈËŁŹčÀŒÆÈ„žĂŸ°ÇűÂĂÓΔğÓĂńÔŒÓжàÉÙÈË?
ÈËŁŹčÀŒÆÈ„žĂŸ°ÇűÂĂÓΔğÓĂńÔŒÓжàÉÙÈË?
![]() Хǿ͏ѧÔȚŒÙÆÚŒäŒÆ»źÓ랞ĞŽÓ
Хǿ͏ѧÔȚŒÙÆÚŒäŒÆ»źÓ랞ĞŽÓ![]() ÎćžöŸ°ÇűÖĐŁŹÈÎŃĄÁœžöÈ„ÂĂÓÎŁŹÇóŃĄÖÁ
ÎćžöŸ°ÇűÖĐŁŹÈÎŃĄÁœžöÈ„ÂĂÓÎŁŹÇóŃĄÖÁ![]() ÁœžöŸ°Çű”ÄžĆÂÊŁŹ(ÒȘÇóÁбíÇóžĆÂÊ)
ÁœžöŸ°Çű”ÄžĆÂÊŁŹ(ÒȘÇóÁбíÇóžĆÂÊ)
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com