
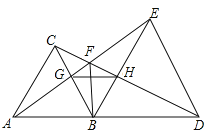
【题目】如图,△ABC和△BDE都是等边三角形,点A,B,D在一条直线上。给出4个结论:①AE=CD;②AB⊥FB;③∠AFC=60°;④△BGH是等边三角形。其中正确的是( )
A.①,②,③B.①,②,④
C.①,③,④D.②,③,④
【答案】C
【解析】
由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BHD≌△BGE,△ABG≌△CHB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
解:①根据题意可知,AB=BC,BE=BD,∠ABC+∠CBE=∠EBD+∠CBE,∴三角形ABE≌三角形CBD,∴AE=CD;
③∵三角形ABE≌三角形CBD,∴∠EAB=∠BCD,∵∠AGB=∠CGF,
∴∠AFC=∠ABC=60°;
④∵∠ABC=∠EBD=60°,
∴∠CBE=60°,
∵AB=BC,∠EAB=∠BCD,
∴三角形AGB≌三角形CHB,
∴GB=BH,
∴三角形BGH为等边三角形;
②设AB⊥FB,则FB⊥AD,易证△ABF≌△DBF,可得AB=BD,显然与已知条件矛盾,故②错误;
故答案为:C.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 在
在![]() 轴正半轴,顶点
轴正半轴,顶点![]() 、
、![]() 分别在
分别在![]() 轴负半轴和正半轴上,
轴负半轴和正半轴上,![]() ,
,![]() ,
,![]()
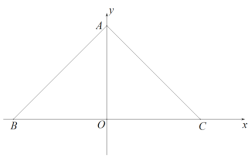
(1)求![]() 的长.
的长.
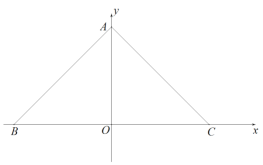
(2)动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 运动的时间为
运动的时间为![]() ,以
,以![]() 为斜边在
为斜边在![]() 右边上方作等腰直角三角形
右边上方作等腰直角三角形![]() ,连接
,连接![]() 、
、![]() ,设
,设![]() 的面积为
的面积为![]() (
(![]() ),求
),求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.
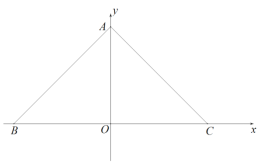
(3)在(2)的条件下,过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于
轴于![]() ,连接
,连接![]() ,当四边形
,当四边形![]() 的面积为
的面积为![]() ,时,求
,时,求![]() 的值及
的值及![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料I:教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则
的两根,则![]() ,
,![]() ,那么
,那么![]() .(请你完成以上的填空)
.(请你完成以上的填空)
阅读材料II:已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)已知![]() 且
且![]() .求
.求![]() 的值;
的值;
![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为_____.
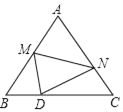
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,对角线AC的垂直平分线EF交AC于O,分别交BC、AD于点E、F.
(1)求证:四边形AECF是菱形;
(2)若AB=4,BC=8,求EC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),设图1中未被这两张正方形纸片覆盖的面积为S1,图2中未被这两张正方形纸片覆盖的面积为S2,当S2-S1=b时,AD-AB的值为( )

A.1B.2C.2a-2bD.b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
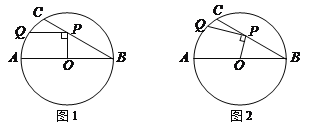
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com