
【题目】阅读材料I:教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则
的两根,则![]() ,
,![]() ,那么
,那么![]() .(请你完成以上的填空)
.(请你完成以上的填空)
阅读材料II:已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)已知![]() 且
且![]() .求
.求![]() 的值;
的值;
![]() ,则
,则![]() .
.
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,有下列说法:
,有下列说法:
①若![]() ,则方程
,则方程![]() 必有一个根为1;
必有一个根为1;
②若方程![]() 有两个不相等的实根,则方程
有两个不相等的实根,则方程![]() 必有两个不相等的实根;
必有两个不相等的实根;
③若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;
成立;
④若![]() 是一元二次方程
是一元二次方程![]() 的根,则
的根,则![]() .
.
其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:宽与长的比是![]() (约为
(约为![]() )的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为
)的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为![]() 的矩形纸片折叠黄金矩形(提示:
的矩形纸片折叠黄金矩形(提示:![]() )
)
第一步:在矩形纸片一端利用图①的方法折出一个正方形,然后把纸片展平.

第二步:如图②,把这个正方形折成两个相等的矩形,再把纸片展平.

第三步:折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图③中所示的
折到图③中所示的![]() 处.
处.

第四步:展平纸片,按照所得的点![]() 折出
折出![]() 使
使![]() 则图④中就会出现黄金矩形.
则图④中就会出现黄金矩形.

问题解决:
(1)图③中![]() _ (保留根号);
_ (保留根号);
(2)如图③,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点
的部分图象如图,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 的值随
的值随![]() 值的增大而增大;⑤当函数值
值的增大而增大;⑤当函数值![]() 时,自变量
时,自变量![]() 的取值范围是
的取值范围是![]() 或
或![]() .其中正确的结论有__________.
.其中正确的结论有__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为![]() ,它各边上格点的个数之和为
,它各边上格点的个数之和为![]() .
.

探究一:图中①—④的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数之和的对应关系如表:
多边形的序号 | ① | ② | ③ | ④ | … |
多边形的面积 | 2 | 2.5 | 3 | 4 | … |
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
![]() 与
与![]() 之间的关系式为:________.
之间的关系式为:________.
探究二:图中⑤—⑧的格点多边形内部都只有2个格点,请你先完善下表格的空格部分(即分别计算出对应格点多边形的面积![]() ):
):
多边形的序号 | ⑤ | ⑥ | ⑦ | ⑧ | … |
多边形的面积 | … | ||||
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
![]() 与
与![]() 之间的关系式为:________.
之间的关系式为:________.
猜想:当格点多边形内部有且只有![]() 个格点时,
个格点时,![]() 与
与![]() 之间的关系式为:_______.
之间的关系式为:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△BDE都是等边三角形,点A,B,D在一条直线上。给出4个结论:①AE=CD;②AB⊥FB;③∠AFC=60°;④△BGH是等边三角形。其中正确的是( )
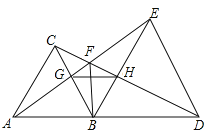
A.①,②,③B.①,②,④
C.①,③,④D.②,③,④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护环境,人人有责”,为了更好的治理好金水河,郑州市污水处理厂决定购买![]() 、
、![]() 两型号污水处理设备共10台,其信息如下表:
两型号污水处理设备共10台,其信息如下表:
单价(万元/台) | 每台处理污水量(吨/月) | |
| 12 | 220 |
| 10 | 200 |
(1)设购买![]() 设备
设备![]() 台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与
台,所需资金共为W万元,每月处理污水总量为y吨,试写出W与![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)经预算,市污水处理厂购买设备的资金不超过106万元,月处理污水量不低于2040吨,请你列举出所有购买方案,并指出哪种方案更省钱,需要多少资金?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com