
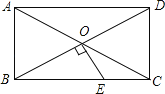
【题目】如图,ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,OE⊥BD交BC于点E,CD=1,则CE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】阅读材料I:教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则
的两根,则![]() ,
,![]() ,那么
,那么![]() .(请你完成以上的填空)
.(请你完成以上的填空)
阅读材料II:已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)已知![]() 且
且![]() .求
.求![]() 的值;
的值;
![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),设图1中未被这两张正方形纸片覆盖的面积为S1,图2中未被这两张正方形纸片覆盖的面积为S2,当S2-S1=b时,AD-AB的值为( )

A.1B.2C.2a-2bD.b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() .
.
(1)求点A、B的坐标;
(2)如图1,P点为y轴正半轴上一点,连接BP,若![]() ,请求出P点的坐标;
,请求出P点的坐标;
(3)如图2,已知![]() ,若C点是x轴上一个动点,是否存在点C,使
,若C点是x轴上一个动点,是否存在点C,使![]() ,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.
,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列的问题:
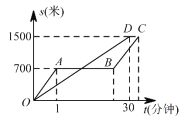
(1)折线OABC表示赛跑过程中__________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_________米;
(2)乌龟用了多少分钟追上正在睡觉的兔子?
(3)兔子醒来,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你计算兔子中间睡觉用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
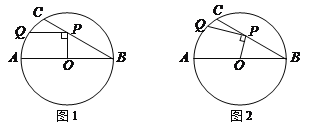
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划用3 800元购进节能灯120只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
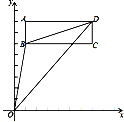
【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com