
【题目】对于一元二次方程![]() ,有下列说法:
,有下列说法:
①若![]() ,则方程
,则方程![]() 必有一个根为1;
必有一个根为1;
②若方程![]() 有两个不相等的实根,则方程
有两个不相等的实根,则方程![]() 必有两个不相等的实根;
必有两个不相等的实根;
③若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;
成立;
④若![]() 是一元二次方程
是一元二次方程![]() 的根,则
的根,则![]() .
.
其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】A
【解析】
按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论,可得答案.
解:①若x=1时,方程ax2+bx+c=0,则a+b+c=0,
∵无法确定a-b+c=0.故①错误;
②∵方程ax2+c=0有两个不相等的实根,
∴△=0-4ac>0
∴-4ac>0
则方程ax2+bx+c=0的判别式,
△=b2-4ac>0
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0
∴c(ac+b+1)=0
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③错误;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:
![]() 或
或![]() ,
,
∴![]() 或
或![]()
∴b24ac=(2ax0+b)2,故④错误.
故选:A.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
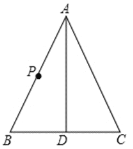
【题目】如图,在△ABC中,AB=AC, AD是△ABC 底边BC上的中线,P为AB上一点.
(1)在AD上找一点E,使得PE+EB的值最小;
(2)若P为AB的中点,当∠BPE= °时,△ABC是等边三角形.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
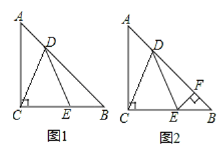
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,E在BC上,且AD=BE,BD=AC.
(1)如图1,求证:DC=DE;
(2)如图2,过E作EF⊥AB于F,若BF=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界上大部分国家都使用摄氏温度(![]() ),但美国、英国等国家的天气预报仍然使用华氏温度(
),但美国、英国等国家的天气预报仍然使用华氏温度(![]() ).两种计量之间有如下对应:
).两种计量之间有如下对应:
摄氏温度( |
|
|
|
|
|
|
华氏温度( |
|
|
|
|
|
|
(1)上表反映了哪两变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(![]() )每提高
)每提高![]() 度,华氏温度(
度,华氏温度(![]() )提高_____度.
)提高_____度.
(3)摄氏温度![]() 度时华氏温度为______度.
度时华氏温度为______度.
(4)华氏温度![]() 度时摄氏温度为_______度.
度时摄氏温度为_______度.
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料I:教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则
的两根,则![]() ,
,![]() ,那么
,那么![]() .(请你完成以上的填空)
.(请你完成以上的填空)
阅读材料II:已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)已知![]() 且
且![]() .求
.求![]() 的值;
的值;
![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com