
����Ŀ���ٶ��̲ģ����볤�ı���![]() ��ԼΪ
��ԼΪ![]() ���ľ��ν����ƽ���Σ��ƽ���θ�������Э�����ȳƵ����У�����������������Ľ�����Ϊȡ����ѵ��Ӿ�Ч�����������˻ƽ���ε���ƣ����������ÿ�Ϊ
���ľ��ν����ƽ���Σ��ƽ���θ�������Э�����ȳƵ����У�����������������Ľ�����Ϊȡ����ѵ��Ӿ�Ч�����������˻ƽ���ε���ƣ����������ÿ�Ϊ![]() �ľ���ֽƬ�۵��ƽ���Σ���ʾ��
�ľ���ֽƬ�۵��ƽ���Σ���ʾ��![]() ��
��
��һ�����ھ���ֽƬһ������ͼ�ٵķ����۳�һ�������Σ�Ȼ���ֽƬչƽ��

�ڶ�������ͼ����������������۳�������ȵľ��Σ��ٰ�ֽƬչƽ��

���������۳��ڲ���εĶԽ���![]() ������
������![]() �۵�ͼ������ʾ��
�۵�ͼ������ʾ��![]() ����
����

���IJ���չƽֽƬ���������õĵ�![]() �۳�
�۳�![]() ʹ
ʹ![]() ��ͼ���оͻ���ֻƽ���Σ�
��ͼ���оͻ���ֻƽ���Σ�

��������
��1��ͼ����![]() _ ���������ţ���
_ ���������ţ���
��2����ͼ�����ж��ı���![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3����д��ͼ�������еĻƽ���Σ���ѡ������һ��˵�����ɣ�
���𰸡���1��![]() ����2�����Σ�����������3���ƽ�����о���
����2�����Σ�����������3���ƽ�����о���![]() ������
������![]() ��������
��������
��������
��1���������֪��NC=BC=2����BCN=90�㣬��AΪNC���е㣬�Ӷ����AC��Ȼ�����ù��ɶ�������������ۣ�
��2�����ݾ��ε����ʺ�ƽ���ߵ����ʿɵ�![]() ,Ȼ������۵������ʿɵ�
,Ȼ������۵������ʿɵ�![]() ���Ӷ�֤��
���Ӷ�֤��![]() ������֤���ı���
������֤���ı���![]() ��ƽ���ı��Σ��ٸ������ε��ж���������֤�����ۣ�
��ƽ���ı��Σ��ٸ������ε��ж���������֤�����ۣ�
��3�����ݻƽ���μ���֤�����ۣ�
�⣺![]() �������֪��NC=BC=2����BCN=90�㣬��AΪNC���е�
�������֪��NC=BC=2����BCN=90�㣬��AΪNC���е�
��AC= ![]() NC=1
NC=1
��AB=![]() =
=![]()
�ʴ�Ϊ��![]() ��
��
![]() �ı���
�ı���![]() ������
������
![]() ��ͼ
��ͼ![]() ���ı���
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]()
![]()
���۵��ã�![]()
![]()
![]()
![]()
![]()
![]() �ı���
�ı���![]() ��ƽ���ı���
��ƽ���ı���
![]()
![]() �ı���
�ı���![]() ������
������
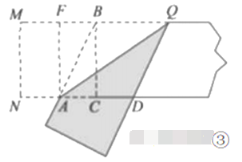
![]() ��ͼ�еĻƽ�����о���
��ͼ�еĻƽ�����о���![]() ������
������![]()
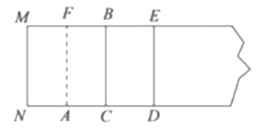
�Ծ���![]() Ϊ������������:
������������:
![]() ��
��
![]() ��
��
��![]()
![]()
![]() ����
����![]() �ǻƽ���Σ�
�ǻƽ���Σ�
�Ծ���![]() Ϊ������������:
������������:
![]() ��AM=2
��AM=2
![]() ��
��
![]()
![]() ����
����![]() �ǻƽ���Σ�
�ǻƽ���Σ�


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��
��a��b����a+b����a2��b2
��a��b����a2+ab+b2����a3��b3
��a��b����a3+a2b+ab2+b3����a4��b4��
������ķ��ֵĹ��ɽ����������
��1����a��b����a4+a3b+a2b2+ab3+b4������ ����ֱ����գ���
��2����a��b����an��1+an��2b+an��3b2��+abn��2+bn��1������ ����ֱ����գ���
��3�����ã�2���еó��Ľ�����62019+62018+��+62+6+1��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��BD=CE��BE=CF������A=50�������DEF�Ķ����ǣ�������
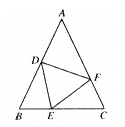
A.75��B.70��C.65��D.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����BD����BD��CD������A��AM��BD�ڵ�M������D��DN��AB�ڵ�N����DN��![]() ����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��_____.
����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼI����![]() �У�
��![]() .��
.��![]() ��
��![]() �⣬����
�⣬����![]() ����
����![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() .��
.��![]() ��ĵ�����ϵ��______��������֤����
��ĵ�����ϵ��______��������֤����
��2����ͼ��![]() ��
��![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��д��
��д��![]() ��ĵ�����ϵ����֤����Ľ���.
��ĵ�����ϵ����֤����Ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ߵ���ʵ������ȫ���Ĺ�ע��ijУѧ����ѧ��ȤС��Ϊ���˽ⱾУͬѧ��ĸ���������ӵ�̬�ȣ���ѧУ��ȡ�˲���ͬѧ�Ը�ĸ�������������ֵ�̬�Ƚ������ʾ����飬����ֱ�Ϊ�dz���ͬ����ͬ������ν������ͬ������̬�ȣ��ֽ�����ͳ�ƽ���Ƴ�����ͼ����ͳ��ͼ����������ͳ��ͼ���ش��������⣺
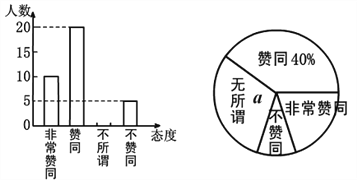
��1��������ʾ�������һ����ȡ��__________��ѧ����a=________%��
��2���벹ȫ����ͳ��ͼ��
��3���֡�����ͬ��̬�ȵ�ѧ�������İٷֱ���ռ���ε�Բ�Ľ�Ϊ__________�ȣ�
��4������У��3000��ѧ����������Ƹ�Уѧ���Ը�ĸ���������ӳ֡���ͬ���͡��dz���ͬ������̬�ȵ�����֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() �Ķ���
�Ķ���![]() ��
��![]() �������ᣬ����
�������ᣬ����![]() ��
��![]() �ֱ���
�ֱ���![]() �Ḻ������������ϣ�
�Ḻ������������ϣ�![]() ��
��![]() ��
��![]()
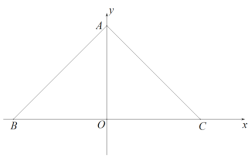
��1����![]() �ij���
�ij���
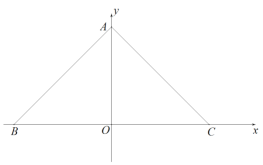
��2������![]() �ӵ�
�ӵ�![]() ������ÿ��
������ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() ���յ�
���յ�![]() �˶�����
�˶�����![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ����
����![]() Ϊб����
Ϊб����![]() �ұ��Ϸ�������ֱ��������
�ұ��Ϸ�������ֱ��������![]() ������
������![]() ��
��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() ������
������![]() ��
��![]() ֮��ĺ�����ϵʽ����ֱ��д���Ա���
֮��ĺ�����ϵʽ����ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
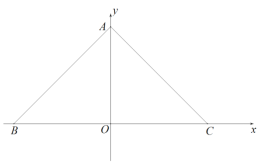
��3���ڣ�2���������£�����![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ����
����![]() ������
������![]() �����ı���
�����ı���![]() �����Ϊ
�����Ϊ![]() ��ʱ����
��ʱ����![]() ��ֵ��
��ֵ��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����I���̲�������ѧϰ��:������![]() ��һԪ���η���
��һԪ���η���![]() ������Ϊ
������Ϊ![]()
![]() ��������һ���ʣ����ǿ��������֪���̹���
��������һ���ʣ����ǿ��������֪���̹���![]() �Ĵ���ʽ��ֵ��
�Ĵ���ʽ��ֵ��
������:
��1����֪![]() Ϊ����
����![]() ����������
����������![]() ��
��![]() ����ô
����ô![]() .(����������ϵ����)
.(����������ϵ����)
�Ķ�����II����֪![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
��:��![]() ��֪
��֪![]()
![]()
![]()
��![]() ��
��![]() ����
����![]()
![]() �Ƿ���
�Ƿ���![]() ��������
��������
![]()
������:
��2����֪![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ�����ABCD�ڣ������ű߳��ֱ�Ϊa��b(a>b)��������ֽƬ��ͼ1��ͼ2���ַ�ʽ����(ͼ1��ͼ2������������ֽƬ���в����ص�)����ͼ1��δ��������������ֽƬ���ǵ����ΪS1��ͼ2��δ��������������ֽƬ���ǵ����ΪS2����S2-S1=bʱ��AD-AB��ֵΪ�� ��

A.1B.2C.2a-2bD.b
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com