练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在中，，和的平分线相交于点，且于点.若，，则的长为（ ）

    A.1B.2C.3D.4

    【答案】A

    【解析】

    根据题意画出图形，连接PC，过点P作PD⊥AC于D，根据角平分线的性质可得PD=PF=PE，利用勾股定理可求出AB的长，根据S△ABC=S△PAB+S△PBC+S△PAC即可求出PE的长．

    如图，连接PC，过点P作PD⊥AC于D，

    ∵点P是∠CAB和∠CBA的平分线的交点，PE⊥AB，

    ∴PD=PF=PE，

    ∵AC=4，BC=3，∠ACB=90°，

    ∴AB==5，

    ∵S△ABC=S△PAB+S△PBC+S△PAC，

    ∴AC·BC=AB·PE+BC·PF+AC·PD，

    ∴AC·BC=（AB+BC+AC）·PE，即3×4=（3+4+5）PE，

    解得：PE=1．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商店用1000元人民币购进水果销售，过了一段时间，又用2400元人民币购进这种水果，所购数量是第一次购进数量的2倍，但每千克的价格比第一次购进的贵了2元．

    （1）该商店第一次购进水果多少千克；

    （2）假设该商店两次购进的水果按相同的标价销售，最后剩下的20千克按标价的五折优惠销售．若两次购进水果全部售完，利润不低于950元，则每千克水果的标价至少是多少元？

    注：每千克水果的销售利润等于每千克水果的销售价格与每千克水果的购进价格的差，两批水果全部售完的利润等于两次购进水果的销售利润之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数的部分图象如图，图象过点，对称轴为直线，下列结论：①；②；③；④当时， 的值随值的增大而增大；⑤当函数值时，自变量的取值范围是或．其中正确的结论有__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC和△BDE都是等边三角形，点A，B，D在一条直线上。给出4个结论：①AE=CD；②AB⊥FB；③∠AFC=60°；④△BGH是等边三角形。其中正确的是（ ）

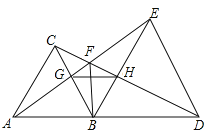
    A.①，②，③B.①，②，④

    C.①，③，④D.②，③，④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E是边AB上的任意一点(不与点A，B重合)，连接DE，作点A关于直线DE的对称点为F，连接EF并延长交BC于点G．

    （1）依题意补全图形，连接DG，求∠EDG的度数；

    （2）过点E作EH⊥DE交DG的延长线于点H，连接BH．线段BH与AE有怎样的数量关系，请写出结论并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“保护环境，人人有责”，为了更好的治理好金水河，郑州市污水处理厂决定购买、两型号污水处理设备共10台，其信息如下表：

    单价（万元/台）

    每台处理污水量（吨/月）

    型

    12

    220

    型

    10

    200

    （1）设购买设备台，所需资金共为W万元，每月处理污水总量为y吨，试写出W与，与之间的函数关系式；

    （2）经预算，市污水处理厂购买设备的资金不超过106万元，月处理污水量不低于2040吨，请你列举出所有购买方案，并指出哪种方案更省钱，需要多少资金？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个工程队共同参与一项筑路工程，甲队单独施工3个月，这时增加了乙队，两队又共同工作了2个月，总工程全部完成，已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月，设甲队单独完成全部工程需个月，则根据题意可列方程中错误的是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】重庆市有五个景区很受游客喜爱，一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计，并根据这个统计结果制作了如下两幅不完整的统计图．

    该小区居民在这次随机调查中被调查到的人数是_______人， 想去景区的人有_________人， 并补全条形统计图．

    被调查到的居民想去 景区旅游的人数最多，若该小区有居民人，估计去该景区旅游的居民约有多少人?

    小强同学赞假期间计划与父母从五个景区中，任选两个去旅游，求选至两个景区的概率，(要求列表求概率)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图1，△ABC为等腰直角三角形，∠ACB=90°，F是AC边上的一个动点（点F与A，C不重合），以CF为一边在等腰直角三角形外作正方形CDEF，连接BF，AD．

    探究展示：（1）①猜想图1中线段BF、AD的数量关系及所在直线的位置关系，直接写出结论；

    ②将图1中的正方形CDEF，绕着点C按顺时针方向旋转任意角度α，得到如图2的情形，图2中BF交AC于点H，交AD于点O，请你判断①中得到的结论是否仍然成立，并选取图2证明你的判断．

    变式练习：（2）将原题中的等腰直角三角形ABC改为直角三角形ABC，∠ACB=90°，正方形CDEF改为矩形CDEF，如图3，且AC=4，BC=3，CD=，CF=1，BF交AC于点H，交AD于点O，连接BD、AF，请判断线段BF、AD所在直线的位置关系，并证明你的判断．

    查看答案和解析>>

    同步练习册答案