
����Ŀ����������![]() ������������ο�ϲ����һ�������ijС������������ڼ�ȥ���������������(ֻѡһ������)����������һ���������ͳ�ƣ����������ͳ�ƽ������������������������ͳ��ͼ��
������������ο�ϲ����һ�������ijС������������ڼ�ȥ���������������(ֻѡһ������)����������һ���������ͳ�ƣ����������ͳ�ƽ������������������������ͳ��ͼ��

![]() ��С�������������������б����鵽��������_______�ˣ�
��С�������������������б����鵽��������_______�ˣ� ![]() ��ȥ
��ȥ![]() ����������_________�ˣ� ����ȫ����ͳ��ͼ��
����������_________�ˣ� ����ȫ����ͳ��ͼ��
![]() �����鵽�ľ�����ȥ �������ε�������࣬����С���о���
�����鵽�ľ�����ȥ �������ε�������࣬����С���о���![]() �ˣ�����ȥ�þ������εľ���Լ�ж�����?
�ˣ�����ȥ�þ������εľ���Լ�ж�����?
![]() Сǿͬѧ���ڼ�ƻ��븸ĸ��
Сǿͬѧ���ڼ�ƻ��븸ĸ��![]() ��������У���ѡ����ȥ���Σ���ѡ��
��������У���ѡ����ȥ���Σ���ѡ��![]() ���������ĸ��ʣ�(Ҫ���б������)
���������ĸ��ʣ�(Ҫ���б������)
���𰸡���1��200��35%��40����ȫ����ͳ��ͼ����������2��B��700����3��![]()
��������
��1������ȥD������������������ռ�İٷֱȵõ���������������ټ�����ȥB�����İٷֱȵõ�m��ֵ��Ȼ��������ȥC������������ȫ����ͳ��ͼ��
��2��������������ͼ���ж���ȥB�������ε�������࣬��2000����m%�ɹ��Ƹþ������εľ����Լ������
��3������״ͼչʾ����12�ֵȿ��ܵĽ�������ҳ�ѡ��B��D���������Ľ������Ȼ����ݸ��ʹ�ʽ���㣮
�⣺��1��20��10%��200��
���Ը�С�������������������б����鵽��������200�ˣ�
m%��![]() ��100%��35%����m��35��
��100%��35%����m��35��
��ȥC����������Ϊ��200��20��70��20��50��40���ˣ���
�ʴ�Ϊ200��35%��40��
��ȫ����ͳ��ͼΪ��

��2�������鵽�ľ�����ȥB�������ε�������࣬
�ʴ�Ϊ��B��
2000��35%��700��
���Թ���ȥ�þ������εľ���Լ��700�ˣ�
��3���б����£�
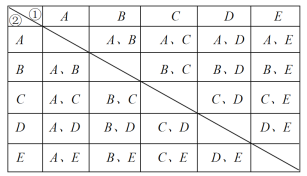
����20�ֵȿ��ܵĽ����������ѡ��B��D���������Ľ����Ϊ2��
����ѡ��B��D���������ĸ��ʣ�![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() �Ķ���
�Ķ���![]() ��
��![]() �������ᣬ����
�������ᣬ����![]() ��
��![]() �ֱ���
�ֱ���![]() �Ḻ������������ϣ�
�Ḻ������������ϣ�![]() ��
��![]() ��
��![]()
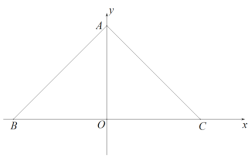
��1����![]() �ij���
�ij���
��2������![]() �ӵ�
�ӵ�![]() ������ÿ��
������ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() ���յ�
���յ�![]() �˶�����
�˶�����![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ����
����![]() Ϊб����
Ϊб����![]() �ұ��Ϸ�������ֱ��������
�ұ��Ϸ�������ֱ��������![]() ������
������![]() ��
��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() ������
������![]() ��
��![]() ֮��ĺ�����ϵʽ����ֱ��д���Ա���
֮��ĺ�����ϵʽ����ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
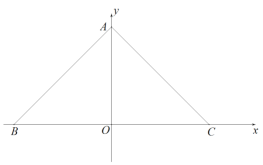
��3���ڣ�2���������£�����![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ����
����![]() ������
������![]() �����ı���
�����ı���![]() �����Ϊ
�����Ϊ![]() ��ʱ����
��ʱ����![]() ��ֵ��
��ֵ��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ��ƽ�����ཻ�ڵ�
��ƽ�����ཻ�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() .��
.��![]() ��
��![]() ����
����![]() �ij��� ��
�ij��� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ�����ABCD�ڣ������ű߳��ֱ�Ϊa��b(a>b)��������ֽƬ��ͼ1��ͼ2���ַ�ʽ����(ͼ1��ͼ2������������ֽƬ���в����ص�)����ͼ1��δ��������������ֽƬ���ǵ����ΪS1��ͼ2��δ��������������ֽƬ���ǵ����ΪS2����S2-S1=bʱ��AD-AB��ֵΪ�� ��

A.1B.2C.2a-2bD.b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��MN��ֱ��AB��CD�ֱ��ڵ�E��F����1���2������
��1�����ж�ֱ��AB��ֱ��CD��λ�ù�ϵ����˵�����ɣ�
��2����ͼ2����BEF���EFD�Ľ�ƽ���߽��ڵ�P��EP��CD���ڵ�G����H��MN��һ�㣬��GH��EG����֤��PF��GH��
��3����ͼ3���ڣ�2���������£�����PH��K��GH��һ��ʹ��PHK����HPK����PQƽ�֡�EPK���ʡ�HPQ�Ĵ�С�Ƿ����仯�������䣬�������ֵ�����仯��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�![]() ��
��![]() ����
����![]() .
.
��1�����A��B�����ꣻ
��2����ͼ1��P��Ϊy����������һ�㣬����BP����![]() �������P������ꣻ
�������P������ꣻ
��3����ͼ2����֪![]() ����C����x����һ�����㣬�Ƿ���ڵ�C��ʹ
����C����x����һ�����㣬�Ƿ���ڵ�C��ʹ![]() �������ڣ���ֱ��д�����з��������ĵ�C�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ���ֱ��д�����з��������ĵ�C�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������O�У�ֱ��AB��6��BC���ң���ABC��30������P��BC�ϣ���Q����O�ϣ���OP��PQ��
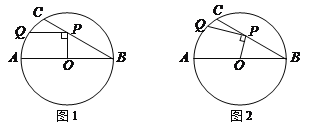
��1����ͼ1����PQ��ABʱ����PQ�ij��ȣ�
��2����ͼ2������P��BC���ƶ�ʱ����PQ�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
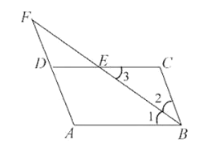
����Ŀ����ͼ�����ı���![]() �У�
�У�![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]()
(1)�![]() ��������
��������![]() �Ƴ�����Ȼ��Ľ�
�Ƴ�����Ȼ��Ľ�
(2)![]() ��
��![]() �����Ϊʲô��
�����Ϊʲô��
(3)֤����![]()
��������������ڣ����������ĸ��ݣ�����������֤����
![]() �� �� ��
�� �� ��
![]() ����֤����
����֤����![]() ���� �� ��
���� �� ��
��![]() ����ƽ���ߵĶ��壩
����ƽ���ߵĶ��壩
![]() �� �� ��
�� �� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com