
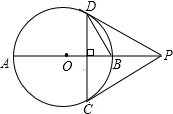
 已知AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,CD⊥AB交⊙O于另一点D,连接PD.
已知AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,CD⊥AB交⊙O于另一点D,连接PD.分析 (1)利用切线的性质和判定,先由性质得到∠OCP=90°,再判断∠ODP=∠OCP即可;
(2)利用切割线定理得到PD2=PB×PA,先算出PA从而求出圆的半径,
(3)利用正弦值设出BE=$\sqrt{5}$x,BD=5x,从而求出DE,再利用三角形角平分线的性质,得出$\frac{DE}{DP}=\frac{BE}{BP}$,求出BP,再用切割线定理PD2=PB×PA=PB(PB+2r),求出圆的半径.
解答 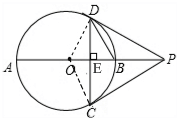 (1)证明:连接OC,OD,
(1)证明:连接OC,OD,
∴OC=OD
∵CD⊥AB,
∴∠COB=∠DOB
∵OP=OP,
∴△OCP≌△ODP(SAS),
∴∠ODP=∠OCP,
∵PC切⊙O于C,
∴OC⊥CP,
∴∠OCP=90°,
∴∠ODP=90°,
∵点D在⊙O上,
∴PD是⊙O的切线.
(2)解:∵PD是⊙O的切线,PBA是⊙O的割线,
∴PD2=PB×PA,
∵PD=3,PB=1,
∴32=1×PA,
∴PA=9,
∴AB=PA-PB=9-1=8,
∴OC=$\frac{1}{2}$AB=$\frac{1}{2}×$8=4,
即:⊙O的半径为4
(3)解:∵sin∠CDB=$\frac{BE}{BD}$=$\frac{\sqrt{5}}{5}$,
∴设BE=$\sqrt{5}$x,BD=5x,
∵CD⊥AB,
∴∠BED=90°,
在Rt△BED中,根据勾股定理,有DE=$\sqrt{{BD}^{2}{-BE}^{2}}$=2$\sqrt{5}$x,
∵PD切⊙O于D,
∠PDB=∠BCD,
AB为⊙O直径,且CD⊥AB,
∴∠BCD=∠BDC,
∴∠BDC=∠PDB,
∴$\frac{DE}{DO}=\frac{BE}{BP}$,
∴$\frac{2\sqrt{5}x}{4}=\frac{\sqrt{5}x}{BP}$,
∴BP=2,
设⊙O的半径为r,
∵PD切⊙O于D,
PAB为⊙O的割线,
∴PD2=PB×PA=PB(PB+2r),
∴42=2(2+2r),
∴r=3.
答:⊙O的半径为3.
点评 本题是中上水平的题,主要考查圆的切线的有关性质和圆的切线的判定,涉的到的知识点比较多,(如圆的切割线定理多次出现,圆中弦切角的性质,三角形的角平分线的性质),第三问不容易想到三角形的角平分线的这个性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
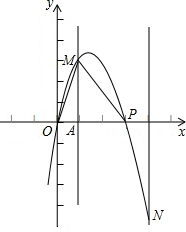 如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位长度的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位长度的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
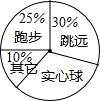 学校为了今年初三年级学生体育中考取得优异的成绩,进行更有针对性的强化训练,体育组为了了解学生最喜欢的考试项目情况,随机抽查了该年级200名学生,调查的结果如图所示.
学校为了今年初三年级学生体育中考取得优异的成绩,进行更有针对性的强化训练,体育组为了了解学生最喜欢的考试项目情况,随机抽查了该年级200名学生,调查的结果如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,CD⊥AB,垂直为点D,F为BC上一点,FG⊥AB,垂足为点G,E为AC上一点,连结DE,且∠1=∠2,求证:DE∥BC.
如图,在△ABC中,CD⊥AB,垂直为点D,F为BC上一点,FG⊥AB,垂足为点G,E为AC上一点,连结DE,且∠1=∠2,求证:DE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com