
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0;②a>0;③b>0; ④c>0; ⑤9a+3b+c<0; ⑥2a+b=0,则其中结论正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
详解:①根据图示知,二次函数与x轴有两个交点,所以![]() ;故①正确;
;故①正确;
②根据图示知,该函数图象的开口向上,
∴a>0;
故②正确;
③又对称轴![]()
∴![]()
∴b<0;
故本选项错误;
④该函数图象交于y轴的负半轴,
∴c<0;
故本选项错误;
⑤根据抛物线的对称轴方程可知:(1,0)关于对称轴的对称点是(3,0);
当x=1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故⑤正确,
⑥对称轴![]()
![]()
即![]() 故本选项正确.
故本选项正确.
正确的有4项.
故选C.
点睛:考查二次函数的图象与系数的关系.二次项系数![]() 决定了开口方向,一次项系数
决定了开口方向,一次项系数![]() 和二次项系数
和二次项系数![]() 共同决定了对称轴的位置,常数项
共同决定了对称轴的位置,常数项![]() 决定了与
决定了与![]() 轴的交点位置.
轴的交点位置.


科目:初中数学 来源: 题型:
【题目】某中学举行春季长跑比赛活动,小明从起点学校西门出发,途经市博物馆后按原路返还,沿比赛路线跑回终点学校西门.设小明离开起点的路程s(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到市博物馆的平均速度是0.3千米/分钟,用时35分钟根据图象提供的信息,解答下列问题:

(1)求图中![]() 的值,并求出
的值,并求出![]() 所在直线方程;
所在直线方程;
(2)组委会在距离起点2.1千米处设立一个拍摄点![]() ,小明从第一次过点
,小明从第一次过点![]() 到第二次经过点
到第二次经过点![]() 所用的时间为68分钟
所用的时间为68分钟
①求![]() 所在直线的函数解析式;
所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-(2a+1)x+b的图象经过(2,-1)和(-2,7)且与直线y=kx-2k-3相交于点P(m,2m-7)
(1) 求抛物线的解析式
(2) 求直线y=kx-2k-3与抛物线y=ax2-(2a+1)x+b的对称轴的交点Q的坐标
(3) 在y轴上是否存在点T,使△PQT的一边中线等于该边的一半?若存在,求出点T的坐标;若不存在,请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;②小华的速度是小明速度的2.5倍;③a=24;④b=480.其中正确的是( )
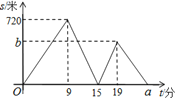
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为8和6的正方形纸片按图1图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.

(1)请用含m的式子表示图1中EF,BF的长;
(2)请用含m,n的式子表示图1,图2中的S1,S2,若m﹣n=3,请问S2﹣S1的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完。设分配给甲店A型产品x件,两商店销售这两种产品每件的利润(元)如下表:
A型利润 | B型利润 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1)分配给乙店B型产品 件(用含x的代数式表示)。
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围。
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则![]() 的值为____________.
的值为____________.
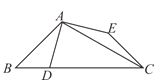
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
(1)求抛物线的解析式;
(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com