
【题目】已知点P是Rt△ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F.
(1)如图1,当点P为AB的中点时,连接AF,BE.求证:四边形AEBF是平行四边形; 
(2)如图2,当点P不是AB的中点,取AB的中点Q,连接EQ,FQ.试判断△QEF的形状,并加以证明. 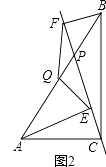
【答案】
(1)证明:如图1,
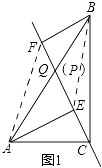
∵点Q为AB中点,∴AQ=BQ.
∵BF⊥CP,AE⊥CP,
∴BF∥AE,∠BFQ=∠AEQ.
在△BFQ和△AEQ中,
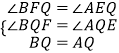 ,
,
∴△BFQ≌△AEQ(AAS).
∴QE=QF.
∴四边形AEBF是平行四边形
(2)证明:△QEF是等腰三角形,如图2,
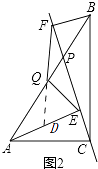
延长FQ交AE于点D,
由(1)知AE∥BF,
∴∠QAD=∠FBQ.
在△FBQ和△DAQ中,
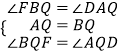 ,
,
∴△FBQ≌△DAQ(ASA),
∴QF=QD.
∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线,
∴QE=QF=QD,即QE=QF,
∴△QEF是等腰三角形
【解析】(1)结合已知证明△BFQ≌△AEQ,进一步得到对角线互相平分即可;(2)延长FQ交AE于点D,证明△FBQ≌△DAQ,结合直角三角形斜边中线等于斜边的一半即可.


科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)若该客户按方案①购买,需付款元(用含x的代数式表示);
若该客户按方案②购买,需付款元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 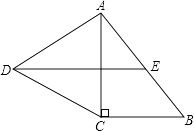
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)计算:3×(﹣2)2﹣|﹣4|﹣6× ![]()
(2)先化简,再求值: ![]() x﹣2(
x﹣2( ![]() x2﹣y2)﹣[2y﹣(x2﹣2y2)],其中x=2,y=﹣4.
x2﹣y2)﹣[2y﹣(x2﹣2y2)],其中x=2,y=﹣4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,正方形ABCD的对角线AC,BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F. 
(1)求证:OE=OF;
(2)若正方形ABCD的对角线长为4,求两个正方形重叠部分的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.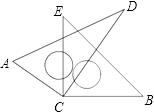
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“水是生命之源”,某城市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
用水量/月 | 单价(元/m3) |
不超过20m3 | 2.8 |
超过20m3的部分 | 3.8 |
另:每立方米用水加收0.2元的城市污水处理费
(1)如果1月份某用户用水量为19m3 , 那么该用户1月份应该缴纳水费元.
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com