
【题目】
(1)计算:3×(﹣2)2﹣|﹣4|﹣6× ![]()
(2)先化简,再求值: ![]() x﹣2(
x﹣2( ![]() x2﹣y2)﹣[2y﹣(x2﹣2y2)],其中x=2,y=﹣4.
x2﹣y2)﹣[2y﹣(x2﹣2y2)],其中x=2,y=﹣4.
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
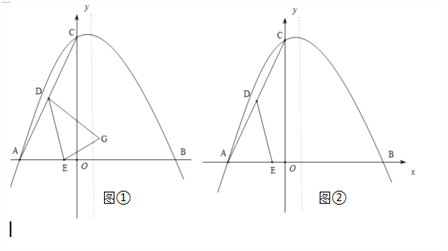
【题目】已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为![]() .
.
(1)求抛物线的解析式;
(2)如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线![]() 的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
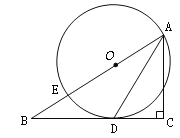
【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形,如图1,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH. 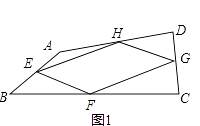
(1)这个中点四边形EFGH的形状是;
(2)如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状并证明. 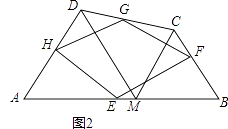
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P是Rt△ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F.
(1)如图1,当点P为AB的中点时,连接AF,BE.求证:四边形AEBF是平行四边形; 
(2)如图2,当点P不是AB的中点,取AB的中点Q,连接EQ,FQ.试判断△QEF的形状,并加以证明. 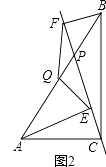
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com