
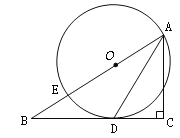
【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=![]() ,求BD的长.
,求BD的长.
【答案】(1)证明见解析;(2)![]()
【解析】(1)连接OD,先根据平行线的判定定理证明OD∥AC,然后依据平行线的性质和等腰三角形的性质证明∠OAD=∠DAC,于是可证明AD平分∠BAC;
(2)连接ED、OD,由题意可知AE=10,接下来,在△ADA中,依据锐角三角形的定义可求得AD的长,然后在△ADC中,可求得DC和AC的长,由OD∥AC可证明△BOD∽△BAC,然后由相似三角形的性质可列出关于BD的方程.
解:(1)如图1,连接OD.
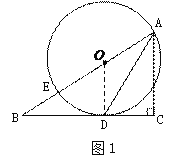
∵⊙O与BC相切于点D,
∴OD⊥BC,
∴∠ODB=90°,
∵∠C=90°,
∴∠C=∠ODB,
∴OD∥AC,
∴∠ODA=∠DAC,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠OAD=∠DAC,
∴AD平分∠BAC.
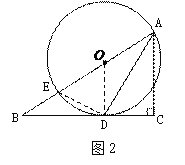
(2)如图2,连接ED.
∵⊙O的直径为10,AE是⊙O的直径,
∴AE=10,∠EDA=90°,
∵∠EAD=∠DAC,sin∠DAC=![]() ,
,
∴sin∠EAD=![]() =
=![]() ,
,
∴DE=![]() ,
,
∴AD=![]() =
=![]() ,
,
同理可求DC=4,AC=8,
∵OD∥AC,
∴△BOD∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:BD=
,解得:BD=![]() .
.
“点睛”本题主要考查的是切线的性质、平行线的判定和性质、等腰三角形的性质、锐角三角函数的定义、相似三角形的判定和性质,列出关于BD的方程是解题的关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)若该客户按方案①购买,需付款元(用含x的代数式表示);
若该客户按方案②购买,需付款元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华购物中心新购进篮球和排球共30个,进价和售价如表,全部销售完后共获利润510元.
篮球 | 排球 | |
进价(元/个) | 95 | 80 |
售价(元/个) | 110 | 100 |
(1)购进篮球和排球各多少个?
(2)销售8个排球的利润与销售几个篮球的利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 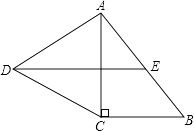
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)计算:3×(﹣2)2﹣|﹣4|﹣6× ![]()
(2)先化简,再求值: ![]() x﹣2(
x﹣2( ![]() x2﹣y2)﹣[2y﹣(x2﹣2y2)],其中x=2,y=﹣4.
x2﹣y2)﹣[2y﹣(x2﹣2y2)],其中x=2,y=﹣4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.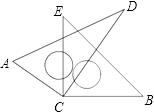
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com