
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.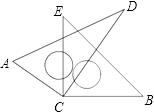
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
【答案】
(1)解:∠ACE=∠BCD,理由如下:
∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
∴∠ACE=∠BCD
(2)解:由余角的定义,得∠ACE=90°﹣∠DCE=90°﹣30°=60°,
由角的和差,得∠ACB=∠ACE+∠BCE=60°+90°=150°
(3)解:∠ACB+∠DCE=180°,理由如下:
由角的和差,得∠ACB=∠BCE+∠ACE,
∠ACB+∠DCE=∠BCE+(∠ACE+DCE)=∠BCE+∠ACE=180°
【解析】 (1)观察图形,根据同角的余角相等,可得出∠ACE+∠DCE=∠BCD+∠DCE=90°,可证得∠ACE=∠BCD。
(2) 根据余角的性质求出∠ACE的度数,再根据∠ACB=∠ACE+∠BCE,计算即可得出答案。
(3)根据图形易证∠ACB=∠BCE+∠ACE,而∠ACE+∠DCE=90°,就可证出∠ACB与∠DCE之和为180°。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为( ![]() ,0),点P为斜边OB上的一动点,则PA+PC的最小值为
,0),点P为斜边OB上的一动点,则PA+PC的最小值为 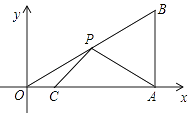
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=![]() ,求BD的长.
,求BD的长.
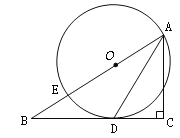
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P是Rt△ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F.
(1)如图1,当点P为AB的中点时,连接AF,BE.求证:四边形AEBF是平行四边形; 
(2)如图2,当点P不是AB的中点,取AB的中点Q,连接EQ,FQ.试判断△QEF的形状,并加以证明. 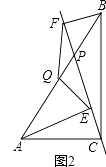
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
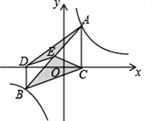
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
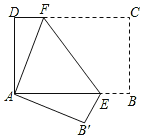
【题目】如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com