
分析 根据移项、合并同类项,可得一元二次方程的一般形式,根据ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项,可得答案.
解答 解:移项、合并同类项,得
4x2-2x=0,
二次项是 4x2,二次项系数是 4,一次项系数是-2,常数项是 0,
故答案为:4x2,4,-2,0.
点评 本题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
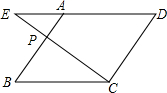 如图,点P是平行四边形ABCD边AB上一点,且AB=3AP,连接CP,并延长CP、DA交于点E,则△AEP与△DEC的周长之比为1:3.
如图,点P是平行四边形ABCD边AB上一点,且AB=3AP,连接CP,并延长CP、DA交于点E,则△AEP与△DEC的周长之比为1:3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
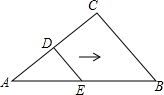 如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为5.
如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
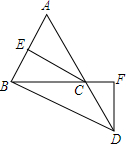 如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且AB=AC.如果∠ABD=105°,∠A=40度.
如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且AB=AC.如果∠ABD=105°,∠A=40度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com