
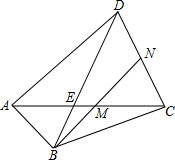
 如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点.
如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点. 分析 延长DA、CB交于点F,如图,设S△ABC=S,则,S△ABD=3S,S△BCD=4S.根据高相等时面积比等于底的比可得$\frac{{S}_{△AFB}}{{S}_{△ABC}}$=$\frac{FB}{BC}$=$\frac{{S}_{△DFB}}{{S}_{△DBC}}$,从而可得S△AFB=S=S△ABC,则有FB=BC.过点B作DF的平行线,交AC于M′,交DC于N′,根据平行线分线段成比例可得:AM′=CM′,DN′=N′C.然后分三种情况讨论(①点M′在点M的左侧,②点M′在点M的右侧,③点M′与点M重合),运用反证法就可解决问题.
解答 证明: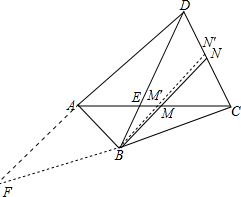 延长DA、CB,交于点F,如图.
延长DA、CB,交于点F,如图.
设S△ABC=S,则,S△ABD=3S,S△BCD=4S.
∵$\frac{{S}_{△AFB}}{{S}_{△ABC}}$=$\frac{FB}{BC}$,$\frac{{S}_{△DFB}}{{S}_{△DBC}}$=$\frac{FB}{BC}$,
∴$\frac{{S}_{△AFB}}{S}$=$\frac{{S}_{△AFB}+3S}{4S}$,
∴S△AFB=S,
∴S△AFB=S△ABC,
∴FB=BC.
过点B作DF的平行线,交AC于M′,交DC于N′,
根据平行线分线段成比例可得:AM′=CM′,DN′=N′C.
①若点M′在点M的左侧,
则$\frac{AM}{AC}$>$\frac{AM′}{AC}$=$\frac{1}{2}$,$\frac{CN}{CD}$<$\frac{CN′}{CD}$=$\frac{1}{2}$,
∴$\frac{AM}{AC}$>$\frac{1}{2}$>$\frac{CN}{CD}$,
与条件“AM:AC=CN:CD”矛盾,故舍去;
②若点M′在点M的右侧,
同理可得$\frac{AM}{AC}$<$\frac{1}{2}$<$\frac{CN}{CD}$,
与条件“AM:AC=CN:CD”矛盾,故舍去;
③若点M′与点M重合,
则$\frac{AM}{AC}$=$\frac{1}{2}$=$\frac{CN}{CD}$,符合条件,
此时M、N分别是AC、DC的中点.
综上所述:M与N分别是AC和CD的中点.
点评 本题主要考查了高相等时面积比等于底的比、平行线分线段成比例等知识,运用反证法是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
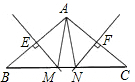 如图,在△ABC中,直线ME垂直平分AB,分别交AB、BC于点E、M,直线NF垂直平分AC,分别交AC、BC于点F、N.求证:△AMN的周长等于BC的长.
如图,在△ABC中,直线ME垂直平分AB,分别交AB、BC于点E、M,直线NF垂直平分AC,分别交AC、BC于点F、N.求证:△AMN的周长等于BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
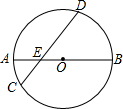 如图,AB是⊙O的直径切AB=8,CD是弦,CD交AB于E,且E为OA的中点,∠BED=45°,
如图,AB是⊙O的直径切AB=8,CD是弦,CD交AB于E,且E为OA的中点,∠BED=45°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com