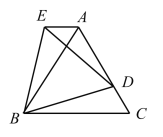
【题目】已知，如图，
和
都是等边三角形，且点
在
上．
（1）求证：
（2）直接写出
和
之间的关系；
科目：初中数学 来源： 题型：
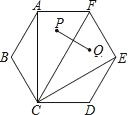
【题目】如图，正六边形ABCDEF中，P、Q两点分别为△ACF、△CEF的内心．若AF=2，则PQ的长度为何？（ ）
A. 1 B. 2 C. 2
﹣2 D. 4﹣2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某共享单车公司提供了手机和会员卡两种支付方式．若用手机支付方式，骑行时间在半小时以内（含半小时）不收费，超出半小时后每半小时收费1元，若选择会员卡支付，骑行时间每半小时收费0.8元，设骑行时间为x小时．
（1）根据题意，填写下表（单位：元）：
骑行时间（小时） | 0.5 | 2 | 3 | … |
手机支付付款金额（元） | 0 | … | ||
会员卡支付付款金额（元） | 3.2 | … |
（2）设用手机支付付款金额为y1元，用会员卡支付付款金额为y2元，分别写出y1，y2关于x的函数关系式；
（3）若李老师经常骑行该公司的共享单车，他应选择哪种支付方式比较合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点D在△ABC边延长线上，点O是边AC上一个动点，过O作直线EF∥BC，交∠BCA的平分线于点F，交∠BCA的外角平分线于E．当点O在线段AC上移动（不与点A，C重合）时，下列结论不一定成立的是（ ）
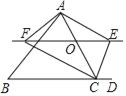
A. 2∠ACE=∠BAC+∠B B. EF=2OC C. ∠FCE=90° D. 四边形AFCE是矩形
查看答案和解析>>
科目：初中数学 来源： 题型：
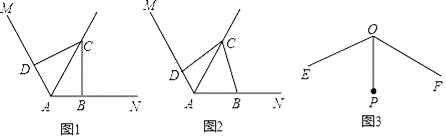
【题目】已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
【发现】
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD= °，△CBD是 三角形；
【探索】
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；
【应用】
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有 ．（只填序号）
①2个②3个③4个④4个以上
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABD≌△CDB，且AB，CD是对应边．下面四个结论中不正确的是( )
A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC，且AD=BC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司为一种新型电子产品在该城市的特约经销商，已知每件产品的进价为40元，该公司每年销售这种产品的其他开支（不含进货价）总计100万元，在销售过程中得知，年销售量y（万件）与销售单价x（元）之间存在如表所示的函数关系，并且发现y是x的一次函数．
销售单价x（元） | 50 | 60 | 70 | 80 |
销售数量y（万件） | 5.5 | 5 | 4.5 | 4 |
（1）求y与x的函数关系式；
（2）问：当销售单价x为何值时，该公司年利润最大？并求出这个最大值；
【备注：年利润=年销售额﹣总进货价﹣其他开支】
（3）若公司希望年利润不低于60万元，请你帮助该公司确定销售单价的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
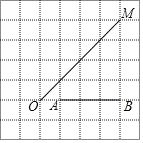
【题目】如图，在每个小正方形的边长为1的网格中，点O，A，B，M均在格点上，P为线段OM上的一个动点．
（1）OM的长等于_______；
（2）当点P在线段OM上运动，且使PA2+PB2取得最小值时，请借助网格和无刻度的直尺，在给定的网格中画出点P的位置，并简要说明你是怎么画的．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
