
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),在
重合),在![]() 同侧分别作等边
同侧分别作等边![]() 和等边
和等边![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,以下五个结论:①
,以下五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,恒成立的结论有( )
,恒成立的结论有( )
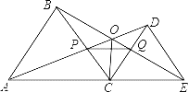
A.①③⑤B.①③④⑤C.①②③⑤D.①②③④⑤
【答案】C
【解析】
①根据全等三角形的判定方法,证出△ACD≌△BCE,即可得出AD=BE.
③先证明△ACP≌△BCQ,即可判断出CP=CQ,③正确;
②根据∠PCQ=60°,可得△PCQ为等边三角形,证出∠PQC=∠DCE=60°,得出PQ∥AE,②正确.
④没有条件证出BO=OE,得出④错误;
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,⑤正确;即可得出结论.
解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,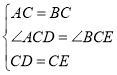 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,结论①正确.
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
又∵∠ACB=∠DCE=60°,
∴∠BCD=180°-60°-60°=60°,
∴∠ACP=∠BCQ=60°,
在△ACP和△BCQ中,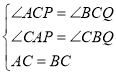 ,
,
∴△ACP≌△BCQ(AAS),
∴CP=CQ,结论③正确;
又∵∠PCQ=60°,
∴△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE,结论②正确.
∵△ACD≌△BCE,
∴∠ADC=∠AEO,
∴∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,
∴结论⑤正确.没有条件证出BO=OE,④错误;
综上,可得正确的结论有4个:①②③⑤.
故选择:C.


科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了取得扶贫工作的胜利,某市对扶贫工作人员进行了扶贫知识的培训与测试,随机抽取了部分人员的测试成绩作为样本,并将成绩划分为![]() 四个不同的等级,绘制成不完整统计图如下图,请根据图中的信息,解答下列问题;
四个不同的等级,绘制成不完整统计图如下图,请根据图中的信息,解答下列问题;
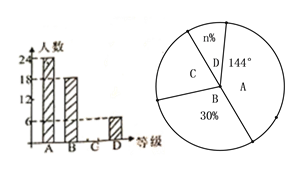
(1)求样本容量;
(2)补全条形图,并填空: ![]() ;
;
(3)若全市有5000人参加了本次测试,估计本次测试成绩为![]() 级的人数为多少?
级的人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填在表示它所在的集合里:
12,![]() ,
,![]() ,
,![]() ,
,![]()
(1)正数集合:{ }; (2)负数集合:{ };
(3)整数集合;{ }; (4)分数集合:{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com